Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js
+ - 0:00:00
Notes for current slide
Notes for next slide

Lesson 5: The Macroeconomics of Development

ECON 317 · Economics of Development · Fall 2019

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/devf19
devF19.classes.ryansafner.com

Growth Models: A History

Working Tools

The Solow (Exogenous) Growth Model

Cross-Country Comparisons

Growth Accounting

Endogenous Growth

Digression: The Economics of Ideas

The Romer Model

Real Productivity

  • The only way to increase income and standards of living (i.e. GDP per capita) is to increase real productivity, the amount of output produced per unit of input (i.e. per work-hour)

Measuring Productivity I

Bureau of Labor Statistics: Labor Productivity and Costs

Real Productivity Increases I

Cox, Michael and Richard Alm, 1999, Myths of Rich and Poor, p. 43

Real Productivity Increases II

Biologically, a human needs approximately 2,500 calories a day to survive, with obvious variations based on height, weight, and sex.

Source: J. Bradford Delong

Real Productivity Increases III

Nordhaus, William D, 1996, "Do Real-Output and Real-Wage Measures Capture Reality?", NBER Working Paper Series

What Causes Productivity (Differences)?

  • Why isn't the whole world equally productive?

  • Different countries have different resources (factors of production)

    • Land, labor, capital, education, technology, etc.

  • Why not take machines and technology from wealthy countries and transfer them to poor countries?

Growth Models: A History

Pre-Classical View: Mercantilism

Thomas Mun

(1571-1641)

"The ordinary means therefore to encrease our wealth and treasure is by Forraign Trade, wherein wee must ever observe this rule; to sell more to strangers yearly than wee consume of theirs in value. [sic]"

Mun, Thomas, 1664, England's Treasure by Forraign Trade or the Ballance of our Forraign Trade is the Rule of our Treasure

Classical Economists on Growth I

Adam Smith

1723-1790

"Nothing, hoever, can be more absurd than this whole doctrine of the balance of trade, upon which, not only these restraints, but almost all the other regulations of commerce are founded...But that trade which, without force or constraint, is naturally and regularly carried on between any two places is always advantageous, though not always equally so, to both," (Book IV, Chapter 3).

"Consumption is the sole end and purpose of all production; and the interest of the producer ought to be attended to only so far as it may be necessary for promoting that of the consumer," (Book IV, Chapter 9)

Smith, Adam, 1776, An Enquiry into the Nature and Causes of the Wealth of Nations

Classical Economists on Growth II

David Ricardo

1772-1823

"A nation is rich, not accordIng to the abundance of its money, nor to the high money value at which its commodities circulate, but according to the abundance of its commodities, contributing to its comforts and enjoyments."

Ricardo, David, 1815, Essay on the Influence of a Low Price of Corn on the Profits of Stock

Classical Economists on Growth III

David Ricardo

1772-1823

"After all the fertile land in the immediate neighbourhood of the first settlers were cultivated, if capital and population increased, more food would be required, and it could only be procured from land not so advantageously situated. Supposing then the land to be equally fertile, the necessity of employing more labourers, horses, &c. to carry the produce from the place where it was grown, to the place where it was to be consumed, although no alteration were to take place in the wages of labour, would make it necessary that more capital should be permanently employed to obtain the same produce." (Book IV, Chapter 9)

"Thus by bringing successively land of a worse quality, or less favourably situated into cultivation, rent would rise on the land previously cultivated, and precisely in the same degree would profits fall; and if the smallness of profits do not check accumulation, there are hardly any limits to the rise of rent, and the fall of profit,"

Ricardo, David, 1815, Essay on the Influence of a Low Price of Corn on the Profits of Stock

Classical Economists on Growth IV

David Ricardo

1772-1823

  • Law of Diminishing Returns: adding more of one factor of production holding others constant will result in successively lower increases in output1

    • Conversely, to get more output, must use more of all factors!

  • Marginal Product of Labor (MPL)=ΔYΔL will eventually decline, holding ˉK,ˉT

  • Marginal Product of Capital (MPK)=ΔYΔK will eventually decline, holding ˉL,ˉT

  • Marginal Product of Land (MPT)=ΔYΔT will eventually decline, holding ˉL,ˉK

1 Note diminishing marginal returns (to one factor) is different from decreasing returns to scale, which is about a less than proportional increase in output from an increase in all factors.

Classical Economists on Growth V

David Ricardo

1772-1823

  • In Ricardo's view, land was a fixed factor
    • Start cultivation on most (agriculturally) productive land first
    • Extend cultivation into worse marginal land and worse marginal land...
    • As more land is used, more and more labor and capital would be needed to increase output (diminishing returns to land)

Classical Economists on Growth VI

David Ricardo

1772-1823

  • Ultimately, marginal product of land would fall to 0 ⟹ economy in a permanent stationary state1
    • Profits to capital fall to 0
    • Wages to laborers fall to subsistence level
    • Rents to land skyrocket due to land being the fixed factor2

1 This pessimism is why people think economics was termed "the dismal science." Its real origin is even stranger, and darker...

2 This is the origin of the idea of a Ricardian (economic) rent - not merely a payment to landowners, but as in "rent-seeking."

Classical Economists on Growth VII

Rev. Thomas Malthus

1766-1834

"Population, when unchecked, increases in a geometrical ratio. Subsistence increases only in an arithmetical ratio. A slight acquaintance with numbers will shew the immensity of the first power in comparison of the second."

"The power of population is so superior to the power of the earth to produce subsistence for man, that premature death must in some shape or other visit the human race."

Malthus, Thomas, 1798, An Essay on the Principle of Population

Classical Economists on Growth VIII

Rev. Thomas Malthus

1766-1834

  • "Malthusian" Trap: finite resources place a hard constraint on population growth

    • When societies grow too large, scarce resources kill off population (famine, disease, warfare)

  • Enormously important concept, we'll explore it in more detail in a later lesson

Malthus, Thomas, 1798, An Essay on the Principle of Population

Classical Economists on Growth IX

Karl Marx

(1818-1883)

  • Surplus value theory

    • Profit can only come from surplus value of labor extracted by capitalists
    • Capitalism will suffer from a "declining average rate of profit"
    • Concentration of capital, reserve army of the unemployed, business cycles

  • Marx's stages in the historical materialist dialectic

    • Proletariat will overthrow Bourgeoisie and usher in Socialism

  • Later (20th Century) Marxist historians:

    • Lenin: Imperialism: The Highest Stage of Capitalism
    • Dependency Theory: the Center (urban, developed countries) exploits the Periphery (rural, developing countries)
      • Developing countries can only develop by breaking free from the Center (West)

Rostow's Stages of Growth

Walt Whitman Rostow

(1916-2003)

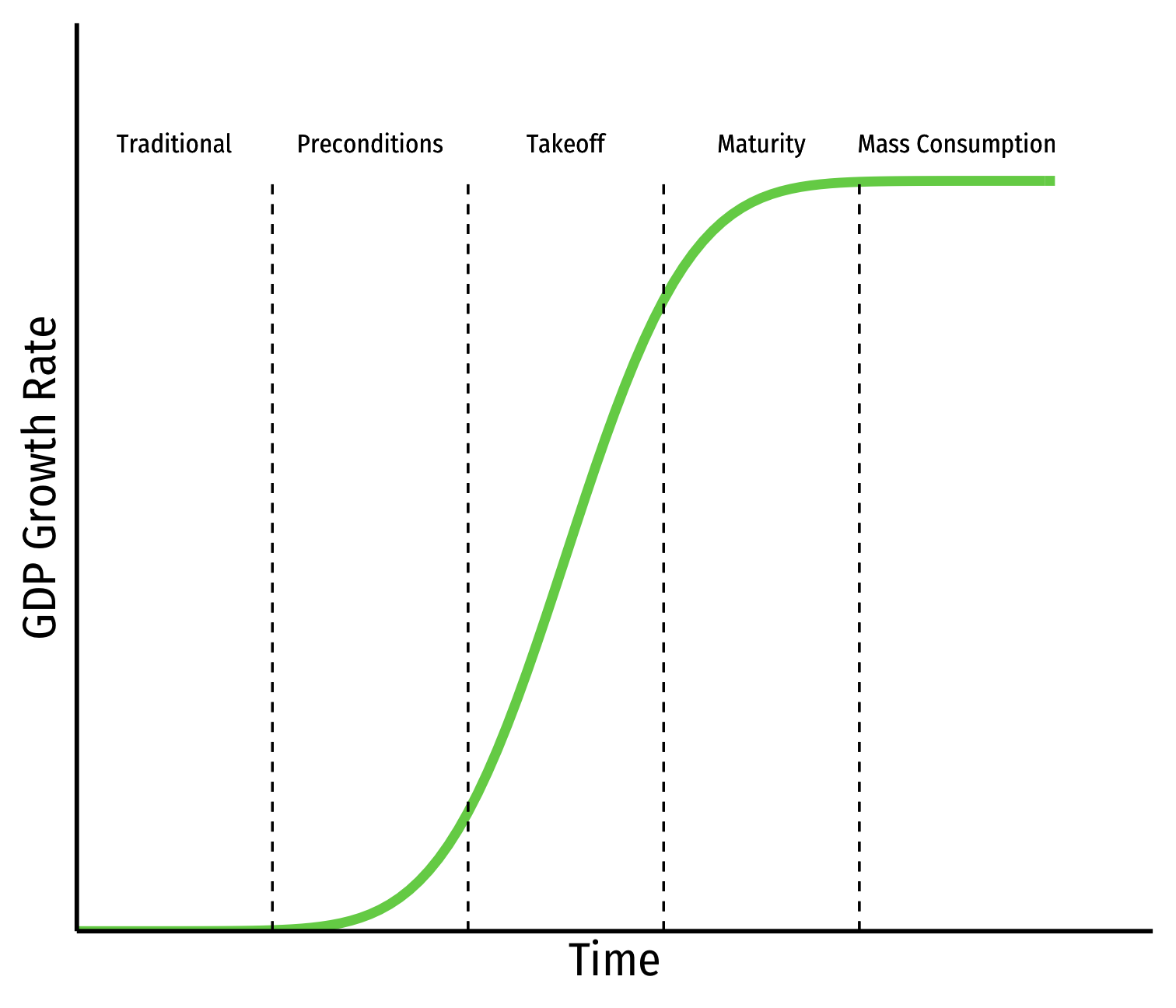
Rostow, W. W, 1960, The Stages of Economic Growth: A Non-Communist Manifesto

The Harrod-Domar Model I

L: Roy Harrod (1900-1978)

R: Evsey Domar (1914-1997)

  • Harrod-Domar Model of economic growth

  • Based off of Keynesian macroeconomic concepts:

    • Marginal Propensity to Save (MPS), ΔSΔY: proportion of (changes in) income saved ∈[0,1]
    • Incremental Capital-Output Ratio (ICOR), ΔKΔY1: addition to capital stock K needed to produce an extra dollar of output Y

  • An economy's equilibrium growth rate =MPSICOR

    • ↑K⟹↑Y⟹↑S
    • We can impute the conditions necessary to yield a desired growth rate

1 Or ΔIΔY, where I is net investment, the change in capital stock.

The Harrod-Domar Model II

L: Roy Harrod (1900-1978)

R: Evsey Domar (1914-1997)

  • "Knife's Edge equilibrium: a single savings rate and ICOR that permits stable growth

    • Growth too low ⟹ depression
    • Growth too high ⟹ hyperinflation

  • Highly simplistic, yet extremely influential

    • Focus on unconsumed surplus to be used for investment
    • GDP growth rate ∝ Investment share of GDP
    • Tendency to think "Development" = Growth = Industrialization
    • Ripe for Development planning from above

The Harrod-Domar Model III

L: Roy Harrod (1900-1978)

R: Evsey Domar (1914-1997)

  • "Financing gap" between "required" investment rate (from model) and a country's actual saving rate

  • Low income countries can't increase savings ⟹ foreign aid from countries with higher savings will lead directly to rapid growth1

1 Remember this argument!

The Harrod-Domar Model IV

William Easterly

1957-

"To sum up, Domar's model was not intended as a growth model, made no sense as a growth model, and was repudiated as a growth model. So it was ironic that Domar's growth model became, and continues to be today, the most widely applied growth model in economic history," (p.28).

Easterly, William, 2010, The Elusive Quest for Growth: Economists Adventures and Misadventures in the Tropics Cambridge: MIT Press

Some Historical Context: 1930s-1960s

Working Tools

An Aggregate Production Function I

  • Aggregate production function: rate at which an economy converts inputs into output1

Y=A∗f(L,K,T)

  • Economists often classify inputs into broad categories:
Factor Owned By Earns
Land (T) Landowners Rent
Labor (L) Laborers Wages
Capital (K) Capitalists Interest
  • "A" is called total factor productivity, augments all factors to improve output
    • Often called "technology" but more like "ideas, incentives, and institutions"

1 Technically this concept is borrowed from microeconomics, where it describes a firm's "technology."

Theoretical Microfoundations I

  • N firms (i=1,2,⋯N) all have the same production technology yi=a∗f(Li,Ki,Ti)
  • All firms minimize cost of production and face the same factor prices:1
    • pL=w=MPL
    • pK=i=MPK
    • pT=r=MPT

1 With the assumption of competitive markets, all factor prices (wages, interest, rents) are equal to the marginal productivity of labor, capital, and land, respectively.

Theoretical Microfoundations II

  • The economy behaves "as if" there is a single firm with technology Y=A∗f(L,K,T) and facing factor prices, where aggregate inputs and output are:

L=l1+l2+⋯+lNK=k1+k2+⋯+kNT=t1+t2+⋯+tNY=y1+y2+⋯+yN

An Aggregate Production Function: Implications

Under constant returns:

  • If two countries have the same technology, there is no economic advantage to size

  • Labor productivity (YL), output-per-worker/hour, is determined only by (KL), capital-per-worker/hour

Y=MPLL+MPKK+MPTT

  • With competitive markets, firms pay each factor its marginal product, firms earn no profits1

1 This is also called the "product exhaustion theorem," and comes from Euler's Theorem for homogeneous functions (constant returns functions are homogeneous of degree 1).

An Aggregate Production Function: Cobb-Douglas I

  • A very common functional form in economics is Cobb-Douglas

Y=AKαL1−α

  • Exponents (α) and (1−α) are "output-elasticities"

    • A 1% increase in K (L) will yield a α% (1−α) increase in Y

  • Constant returns to scale1: a k% increase in all factors of production will yield a k% increase in Y

  • More about Cobb-Douglas functions

Y=K0.5L0.5

1 Only when all exponents sum to 1. In technical terms, the production function is "homogeneous of degree 1"

An Aggregate Production Function: Cobb-Douglas I

Y=AKαL1−α

  • GDP (Y): "Total Output" = "Total Income" for all factor-owners

  • Exponents α and (1−α) are the Factor Shares of National Income

    • α: capital's share of national income
    • (1−α): labor's share of national income

  • Empirically, very stable:

    • Capital's share: α≈0.3
    • Labor's share: 1−α≈0.7

Y=K0.3L0.7

Aggregate Production Function: Labor I

  • Look at Labor, holding other factors constant:1

Example: When ˉK=9

Y=3L0.5

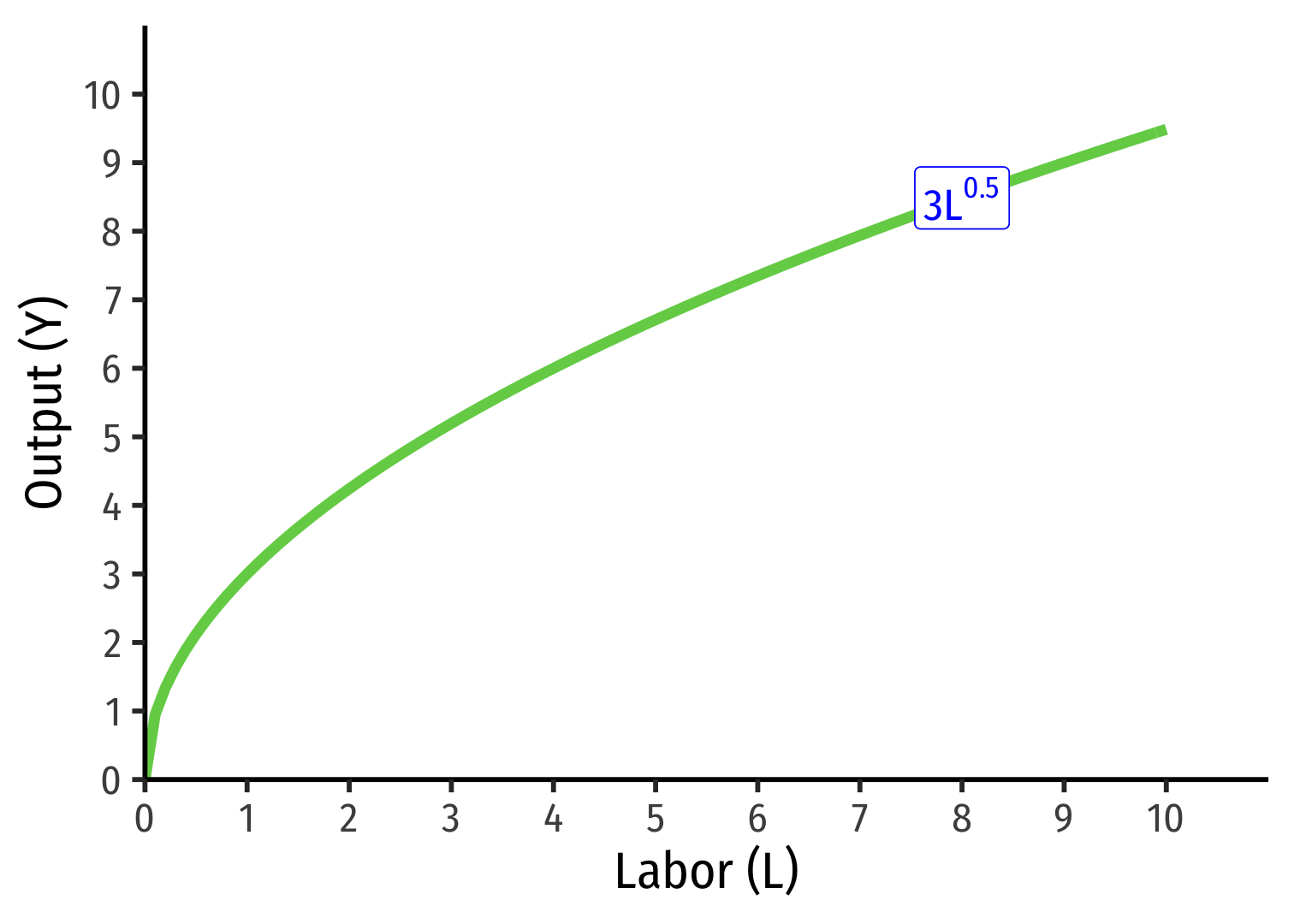
1 We often consider "the short run" where K is fixed, and production functions are simply functions of labor with fixed capital y=f(ˉk,l).

Aggregate Production Function: Labor II

  • Look at Labor, holding other factors constant:

  • The marginal product of labor: the additional output produced by an additional unit of labor (holding other factors constant)

MPL=ΔYΔL

  • The average product of labor: output per worker

APL=YL

Aggregate Production Function: Capital I

  • Look at Capital, holding other factors constant:

Example: When ˉL=9

Y=3K0.5

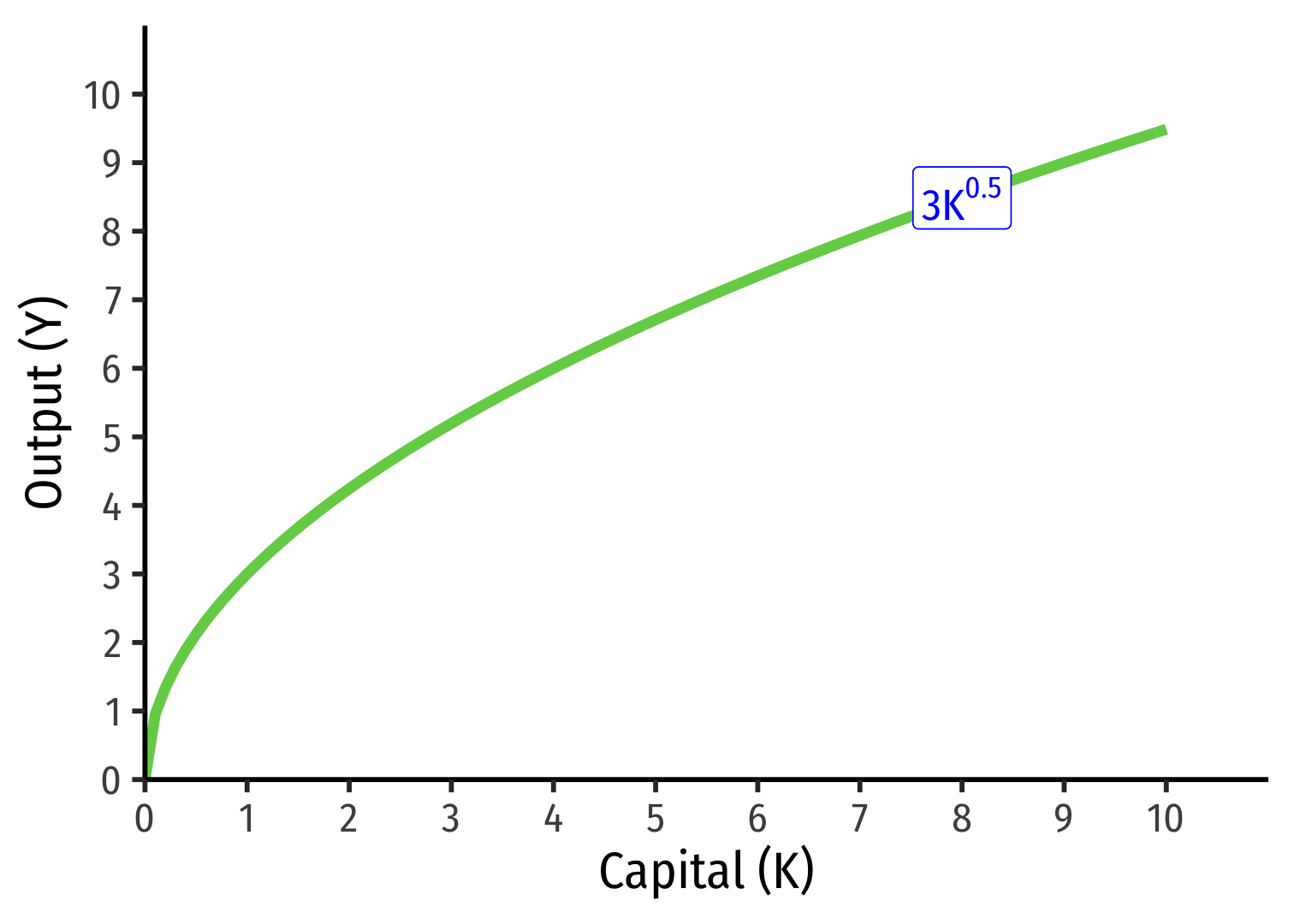
Aggregate Production Function: Capital II

  • The marginal product of capital: the additional output produced by an additional unit of capital (holding other factors constant)

MPK=ΔYΔK

  • The average product of capital: output per unit of capital

APK=YK

1 This is ∂Y∂K.

Capital and Labor

  • Often compare capital-to-labor ratio (KL)

  • Capital "widening": stock of capital increases, but capital per worker (KL) does not change

    • Increase in K is same rate as increase in labor and depreciation

  • Capital "deepening": stock of capital per worker (KL) is increasing

The Solow Model (Exogenous Growth)

Kaldor's Stylized Facts About Growth

Nicholas Kaldor

(1908-1986)

"A satisfactory model concerning the nature of the growth process in a capitalist economy must also account for the remarkable historical constancies revealed by recent empirical investigations." (p.591)

  1. Output per worker grows over time

  2. Capital per worker grows over time

  3. The capital-to-output ratio is approximately constant over time

  4. Capital and labor's share of output is approximately constant over time

  5. The return to capital is approximately constant over time

  6. Levels of output per person vary widely across countries

Kaldor, Nicholas, 1957, "A Model of Economic Growth," Economic Journal 67(268): 591-624

The Solow (Neoclassical) Growth Model

Robert Solow

(1924-)

Economics Nobel 1987

"All theory depends on assumptions which are not quite true. That is what makes it theory. The art of successful theorizing is to make the inevitable simplifying assumptions in such a way that the final results are not very sensitive," (p.65)

"The characteristic and powerful conclusion of the Harrod-Domar line of thought is that even for the long run the economic system is at best balanced on a knife-edge of equilibrium growth...The bulk of [Solow's] paper is devoted to a model of long-run growth which accepts all of the Harrod-Domar assumptions [but] instead I suppose that [output] is produced by labor and capital under the standard neoclassical conditions," (pp.65-66)

Solow, Robert, 1956, "A Contribution to the Theory of Economic Growth," Quarterly Journal of Economics 70(1): 65-94

The "Simple" Solow Model: Key Assumptions

  • An aggregate Cobb-Douglas production function
  • Diminishing MPK
  • Can accumulate physical capital (K)
  • Technology grows exogenously

  • Constant rate of Savings and of Investment (s)

  • I am going to leave out excess parts of the model: role of taxes, interest rates, etc, on consumption, saving, and investment1

1 This isn't a macroeconomics course!

The "Simple" Solow Model: Equations

  • Ct+It=Yt=f(K,L)
    • Income is equal to consumption plus investment
    • Output is equal to the production function
    • Income = Output

The "Simple" Solow Model: Equations

  • Ct+It=Yt=f(K,L)
    • Income is equal to consumption plus investment
    • Output is equal to the production function
    • Income = Output
  • It=sf(Kt,Lt)
    • Investment is equal to the fraction of income (output) saved s times output

The "Simple" Solow Model: Equations

  • Ct+It=Yt=f(K,L)
    • Income is equal to consumption plus investment
    • Output is equal to the production function
    • Income = Output
  • It=sf(Kt,Lt)
    • Investment is equal to the fraction of income (output) saved s times output
  • Kt+1=Kt(1−δ)+It
    • The stock of capital K changes over time from depreciation (δ) and new investment It

The "Simple" Solow Model: Equations

  • Ct+It=Yt=f(K,L)
    • Income is equal to consumption plus investment
    • Output is equal to the production function
    • Income = Output
  • It=sf(Kt,Lt)
    • Investment is equal to the fraction of income (output) saved s times output
  • Kt+1=Kt(1−δ)+It
    • The stock of capital K changes over time from depreciation (δ) and new investment It
  • Lt=L
    • The stock of labor is constant over time

The "Simple" Solow Model: Implications

  • Kt+1=Kt(1−δ)+sf(Kt,Lt)
    • Plugging equation 2 into equation 3

The "Simple" Solow Model: Implications

  • Kt+1=Kt(1−δ)+sf(Kt,Lt)
    • Plugging equation 2 into equation 3
  • Steady-State equilibrium: δK=sf(K,L)
    • Amount of capital depreciation is the same as the amount saved & invested

Equations and Implications, in Terms of k

  • Restate model in terms of k≡KL, i.e. divide everything by L to get "per worker"
    • y=YL, output per worker
    • k=KL, capital per worker

Equations and Implications, in Terms of k

  • Restate model in terms of k≡KL, i.e. divide everything by L to get "per worker"
    • y=YL, output per worker
    • k=KL, capital per worker

  1. ct+it=yt=f(kt)

  2. it=sf(kt)

  3. kt+1=kt(1−δ)+it

Equations and Implications, in Terms of k

  • Restate model in terms of k≡KL, i.e. divide everything by L to get "per worker"
    • y=YL, output per worker
    • k=KL, capital per worker

  1. ct+it=yt=f(kt)

  2. it=sf(kt)

  3. kt+1=kt(1−δ)+it

  • Implications

  1. kt+1=kt(1−δ)+sf(kt)

  2. Steady-State equilibrium: δk=sf(k)

The "Simple" Model Graphically: Capital and Depreciation I

  • Whenever Investment > Depreciation:
    • Capital stock is growing over time, gK>0
    • Adding more new capital than is lost to depreciation
    • Movement to the right on graph k→

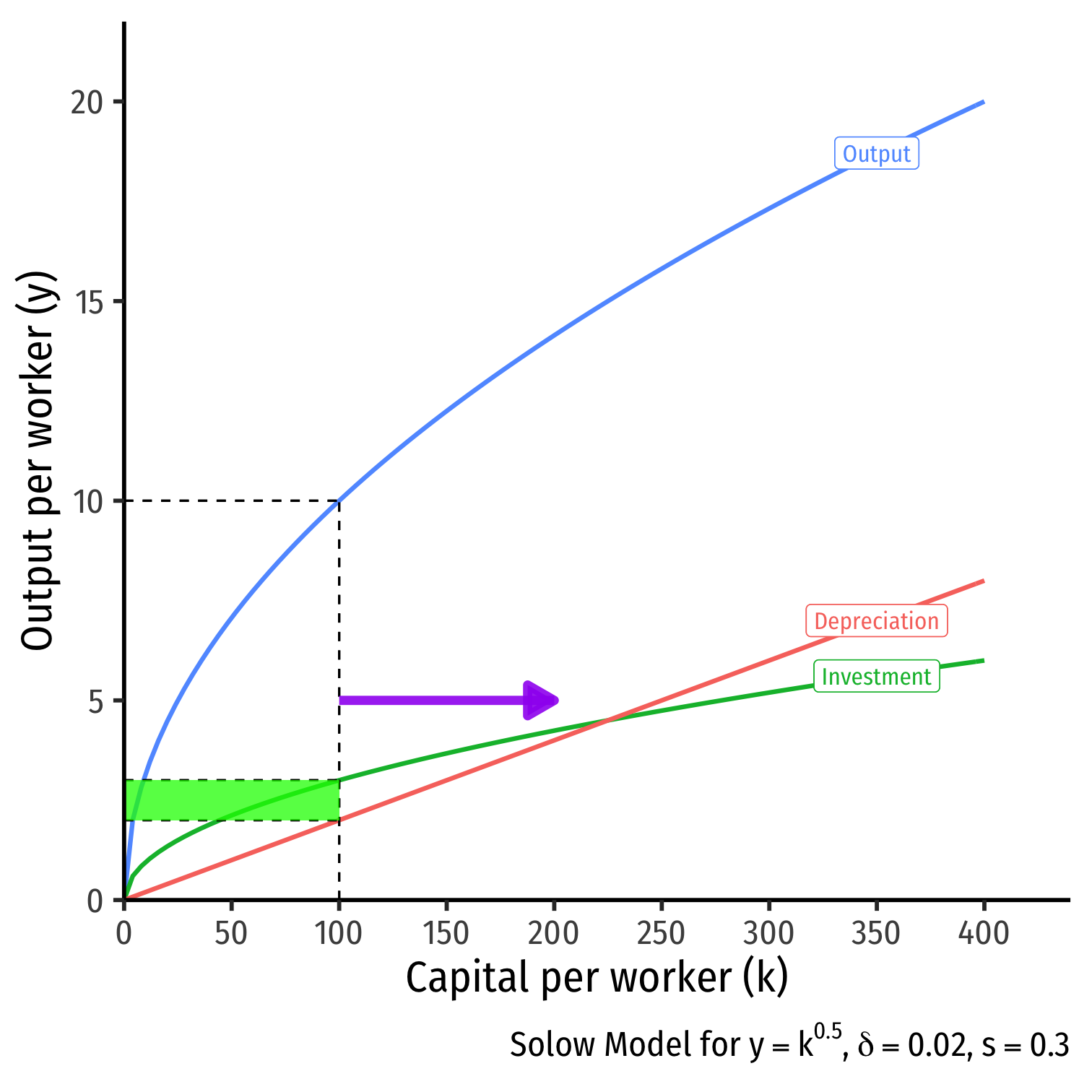
The "Simple" Model Graphically: Capital and Depreciation II

  • Whenever Investment < Depreciation:
    • Capital stock is shrinking over time, gK<0
    • Adding less new capital than is lost to depreciation
    • Movement to the left on graph ←k

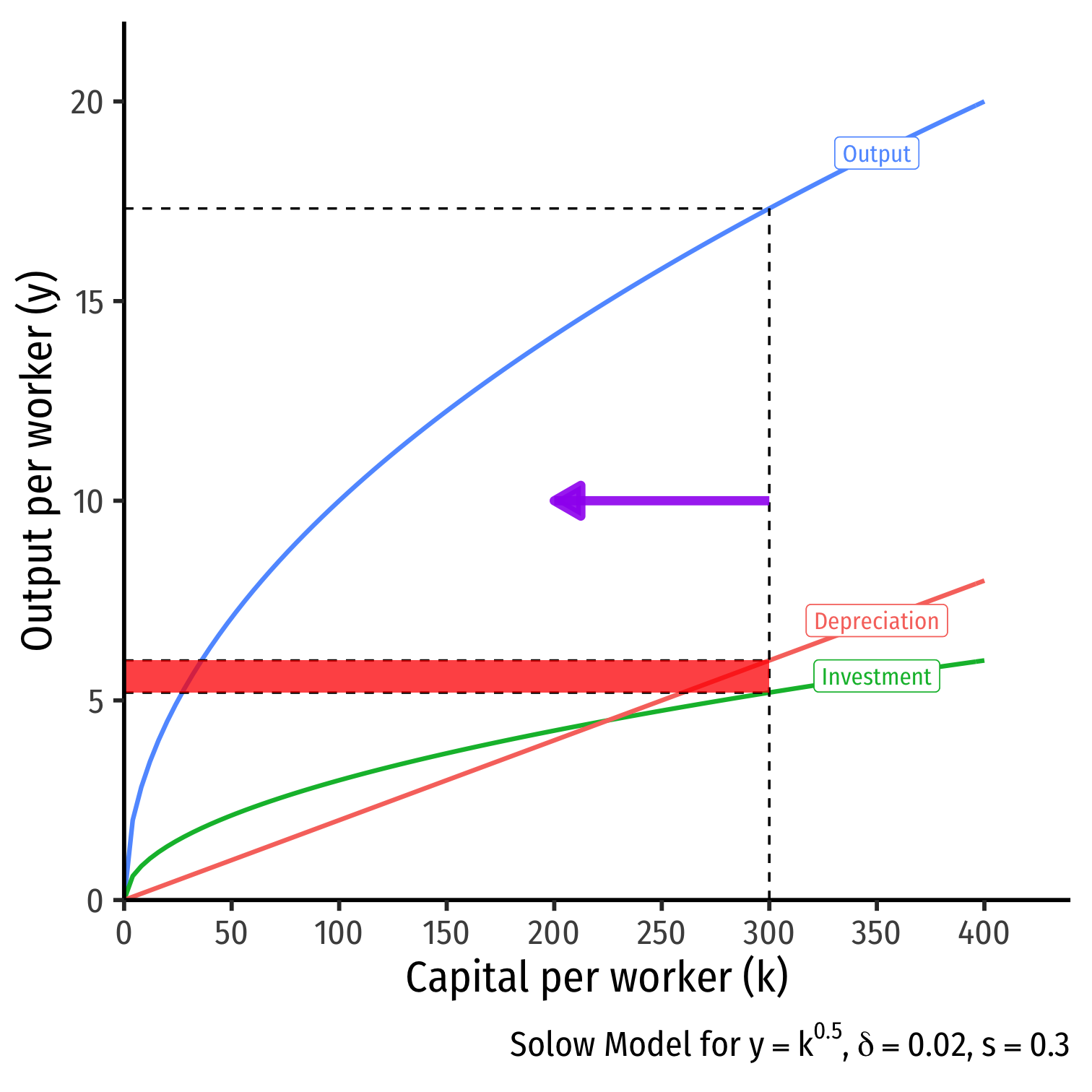
The "Simple" Model Graphically: Capital & the Steady State

  • Whenever Investment = Depreciation

    • Capital stock reaches a steady state, gK=0
    • Adding exactly as much new capital that is lost to depreciation
    • No movement on graph

  • Steady State level of capital: k∗t:sf(kt)=δkt,gk=0

  • Steady State level of output

    • Amount available for consumption, c∗t=y∗t−i∗t

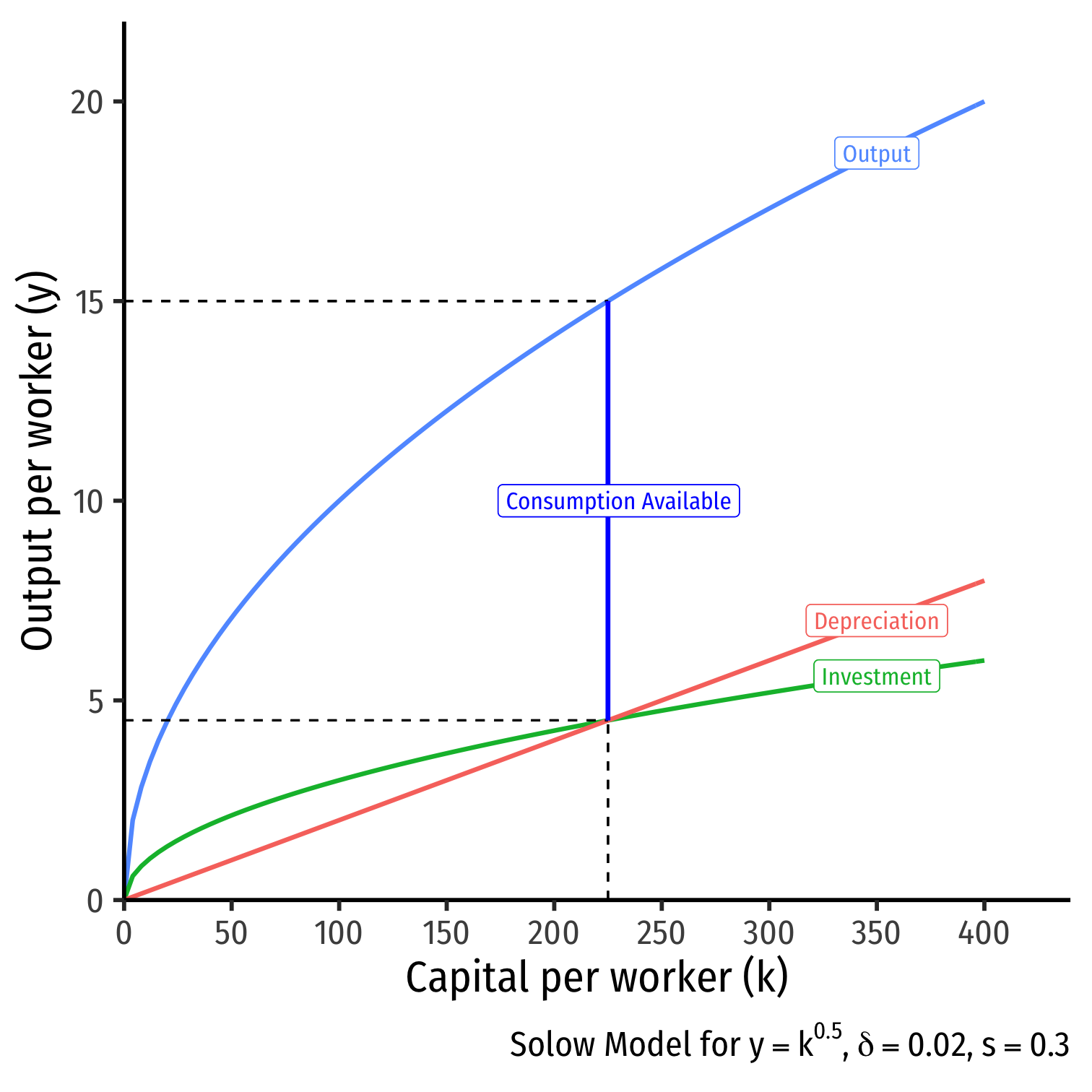
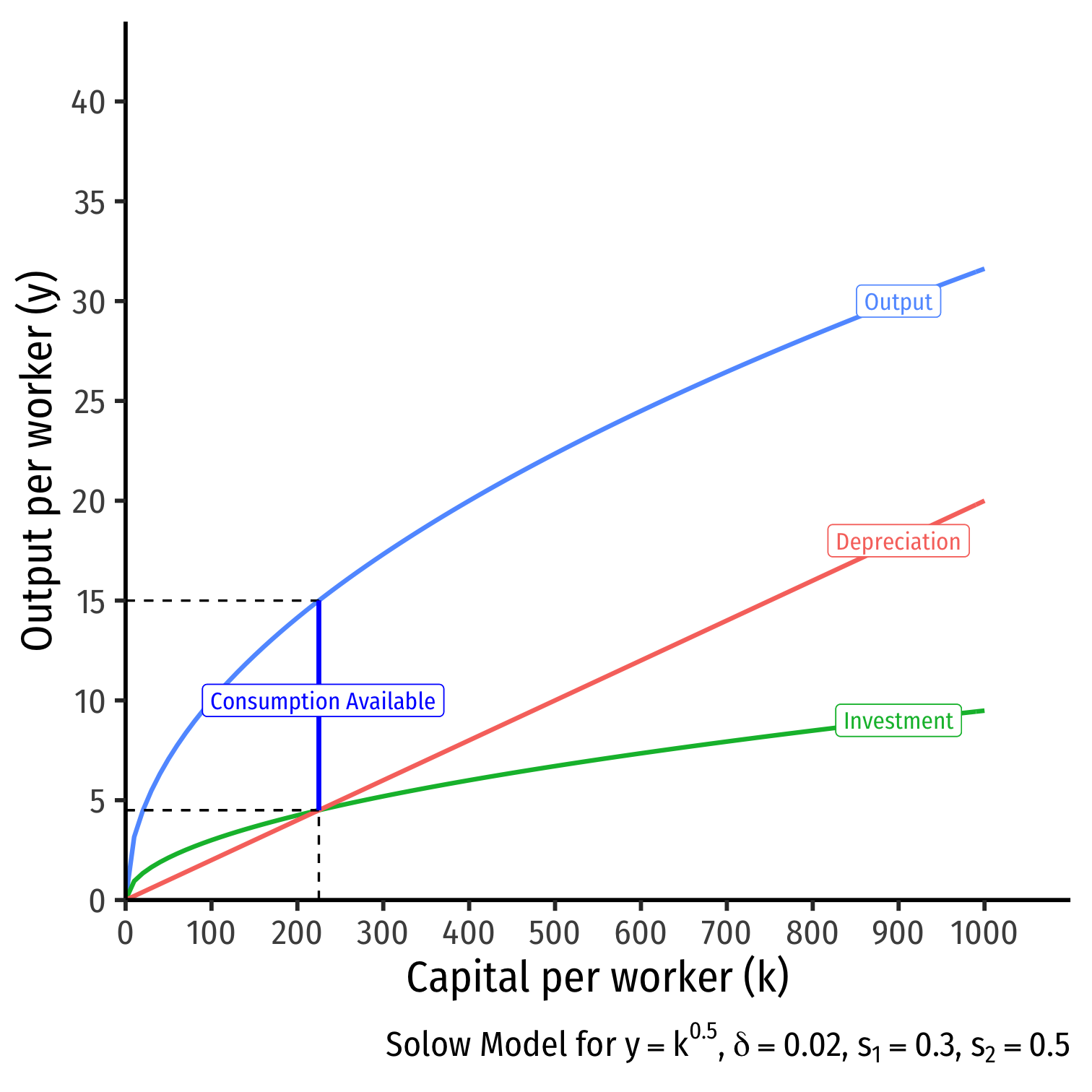
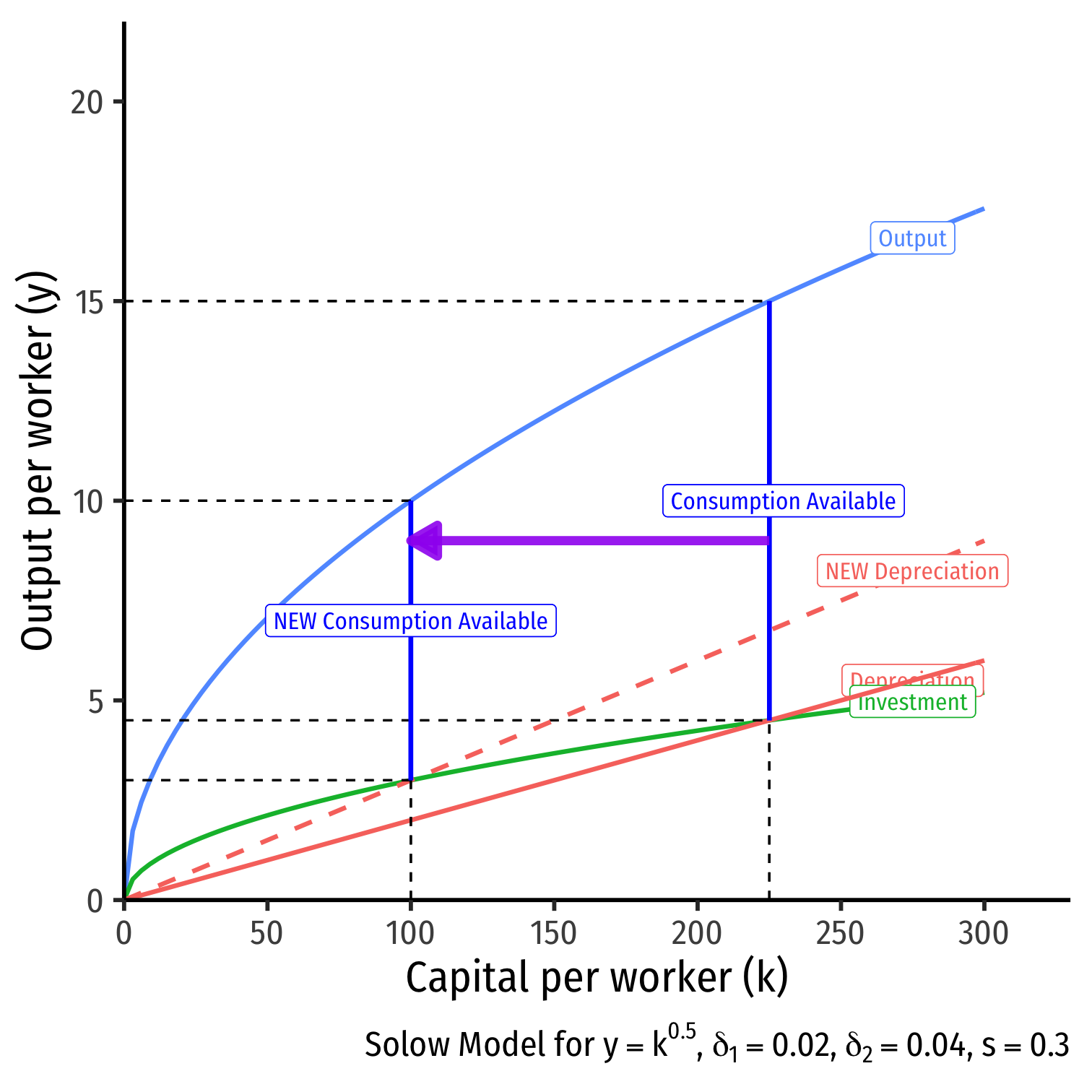
Comparative Statics: A Change in Savings I

  • What if consumers decide to save more?
    • s1=0.30
    • s2=0.50

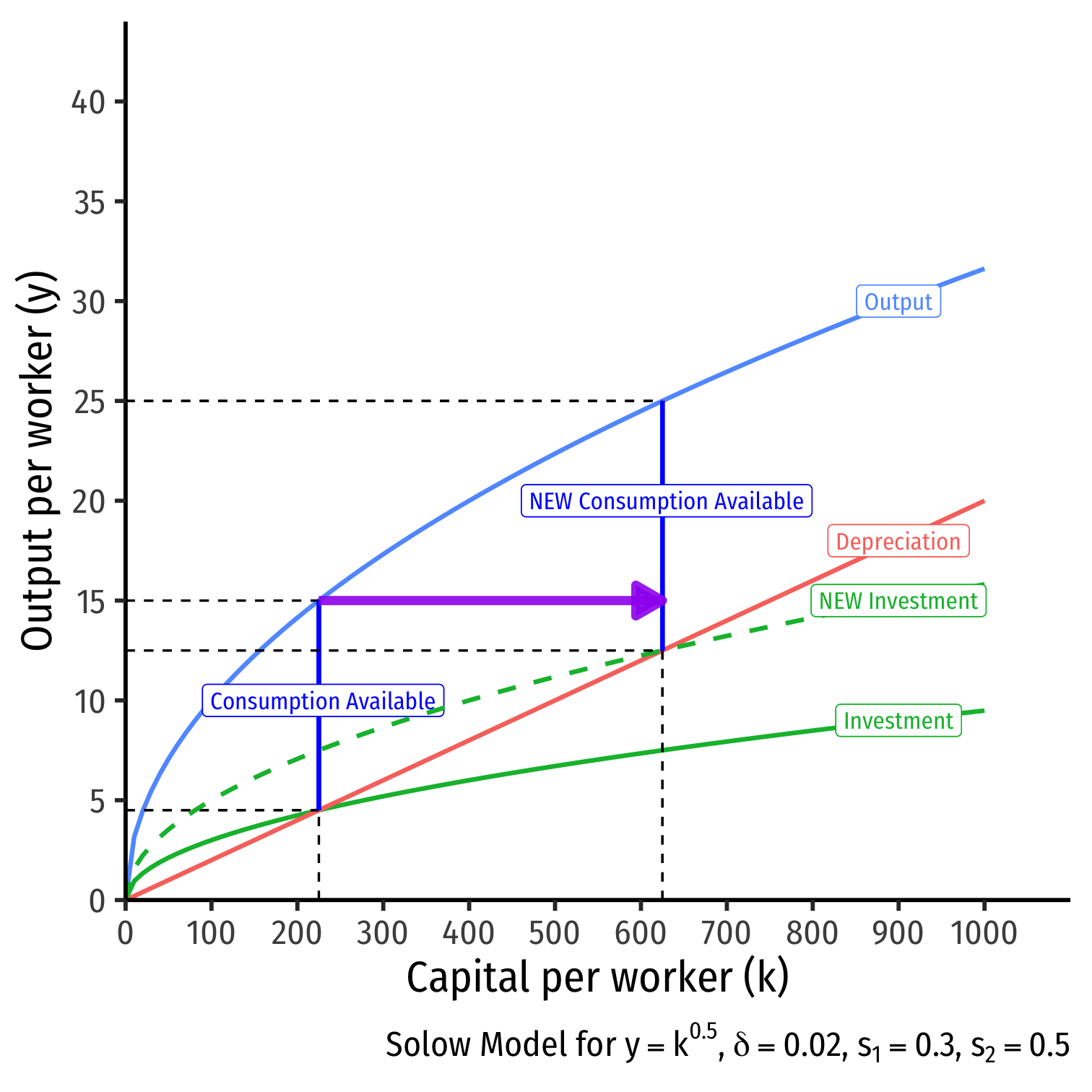
Comparative Statics: A Change in Savings II

  • What if consumers decide to save more?

    • s1=0.30
    • s2=0.50

  • Investment it increases

  • Steady state level of capital k∗t increases

  • Steady state output increases y∗t

  • Steady state amount of consumption

    • Decreases at first from more savings
    • Increases from more output produced

Comparative Statics: A Change in Depreciation I

  • What if depreciation costs increase?
    • δ1=0.02
    • δ2=0.04

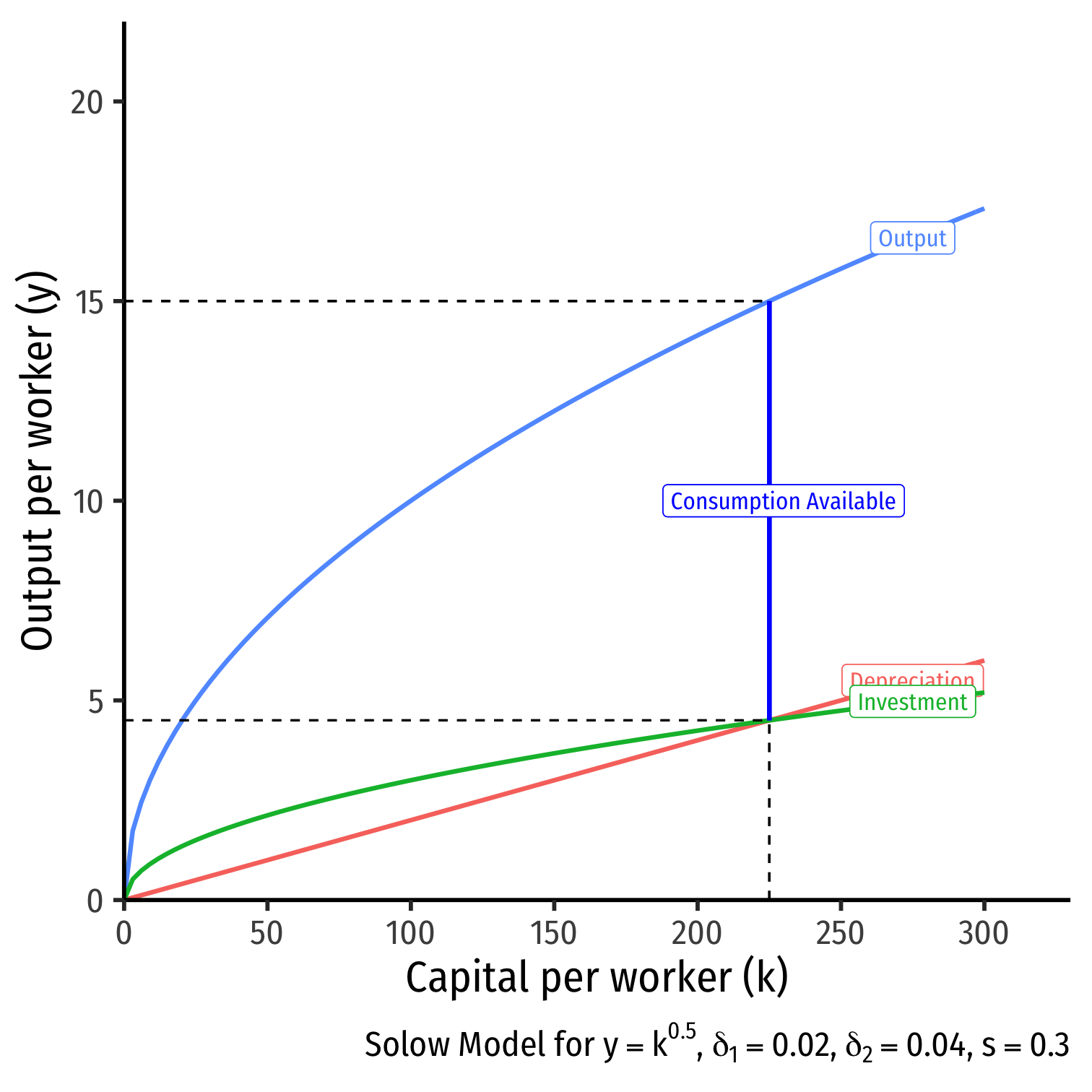
Comparative Statics: A Change in Depreciation II

  • What if depreciation costs increase?

    • δ1=0.02
    • δ2=0.04

  • Investment it decreases

  • Steady state level of capital k∗t decreases

  • Steady state output decreases y∗t

  • Steady state amount of consumption c∗t decreases

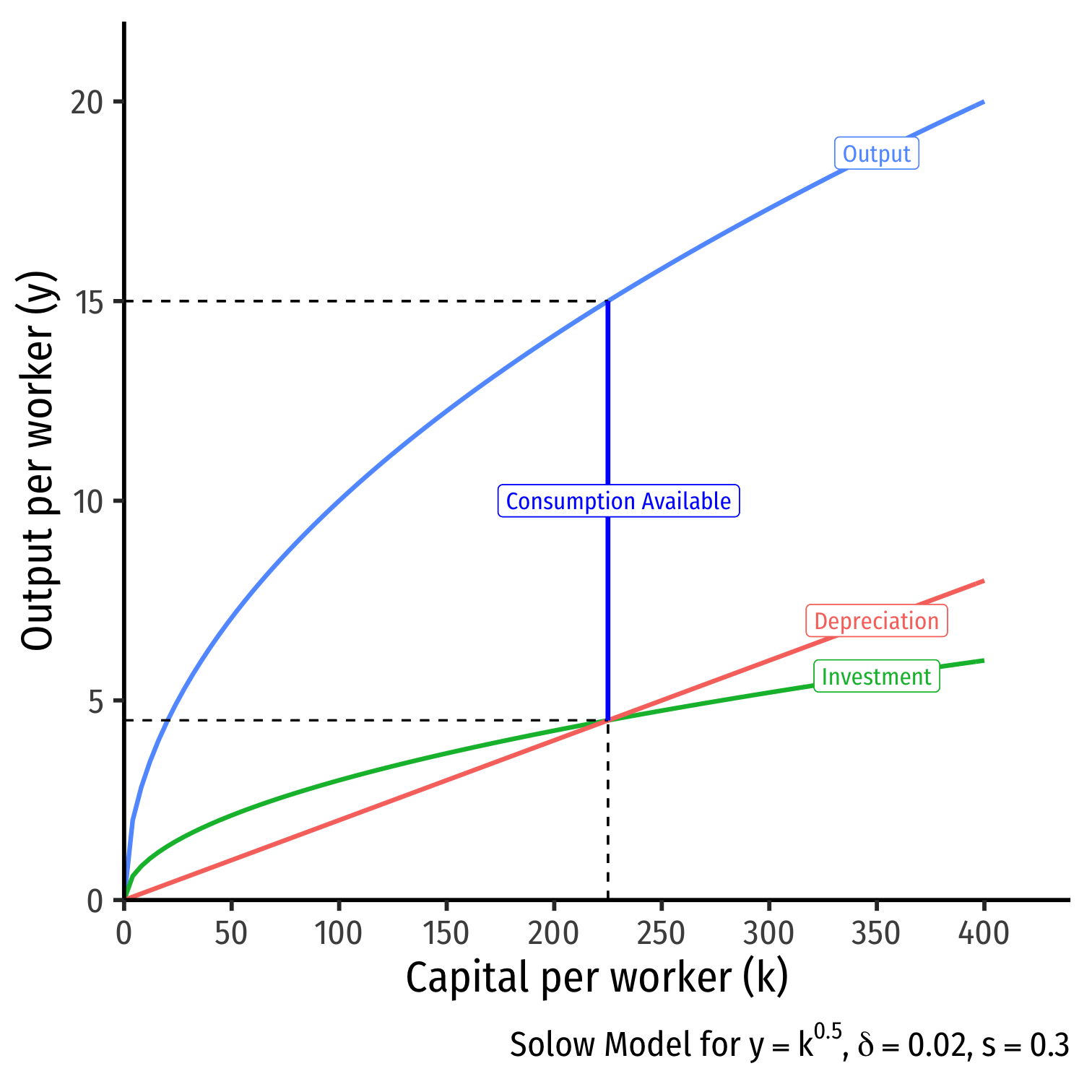
The Golden Rule Level of k I

  • Different values of s lead to different steady state levels of k∗, which is best?

  • The best steady state is one where there is the highest possible consumption per person c∗=(1−s)f(k∗)

  • Increase in s

    • Reduces consumption's share of income (1−s)
    • Results in higher k∗ and higher y∗

  • Find the value of s (and k∗) that maximize c∗

The Golden Rule Level of k II

maxc∗c∗=f(k∗)⏟y∗−δk∗⏟=i∗ in SS

dc∗dk∗=df(k∗)dk∗−dδk∗dk∗0=MPK−δMPK=δ

  • Golden Rule level of k∗GR where slope of depreciation line = slope of production function, f(k∗)

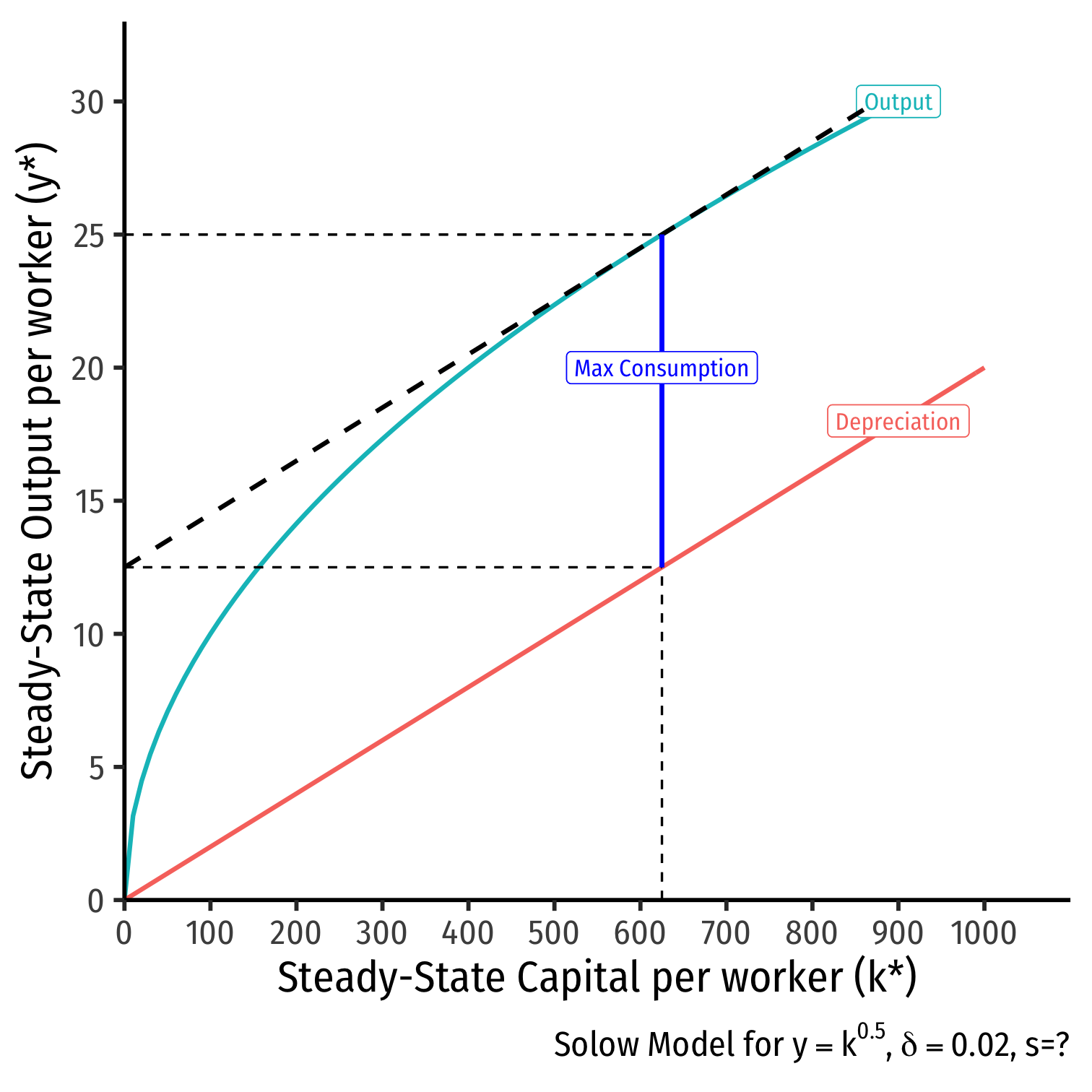
The Golden Rule Level of k III

  • Golden Rule level of k∗GR where slope of depreciation line = slope of production function, f(k∗)

  • Golden Rule level of sGR=δk∗GRy∗GR

    • In this example, sGR=0.02(625)25=0.50

  • Optimal level of savings is 0.50 or 50%!

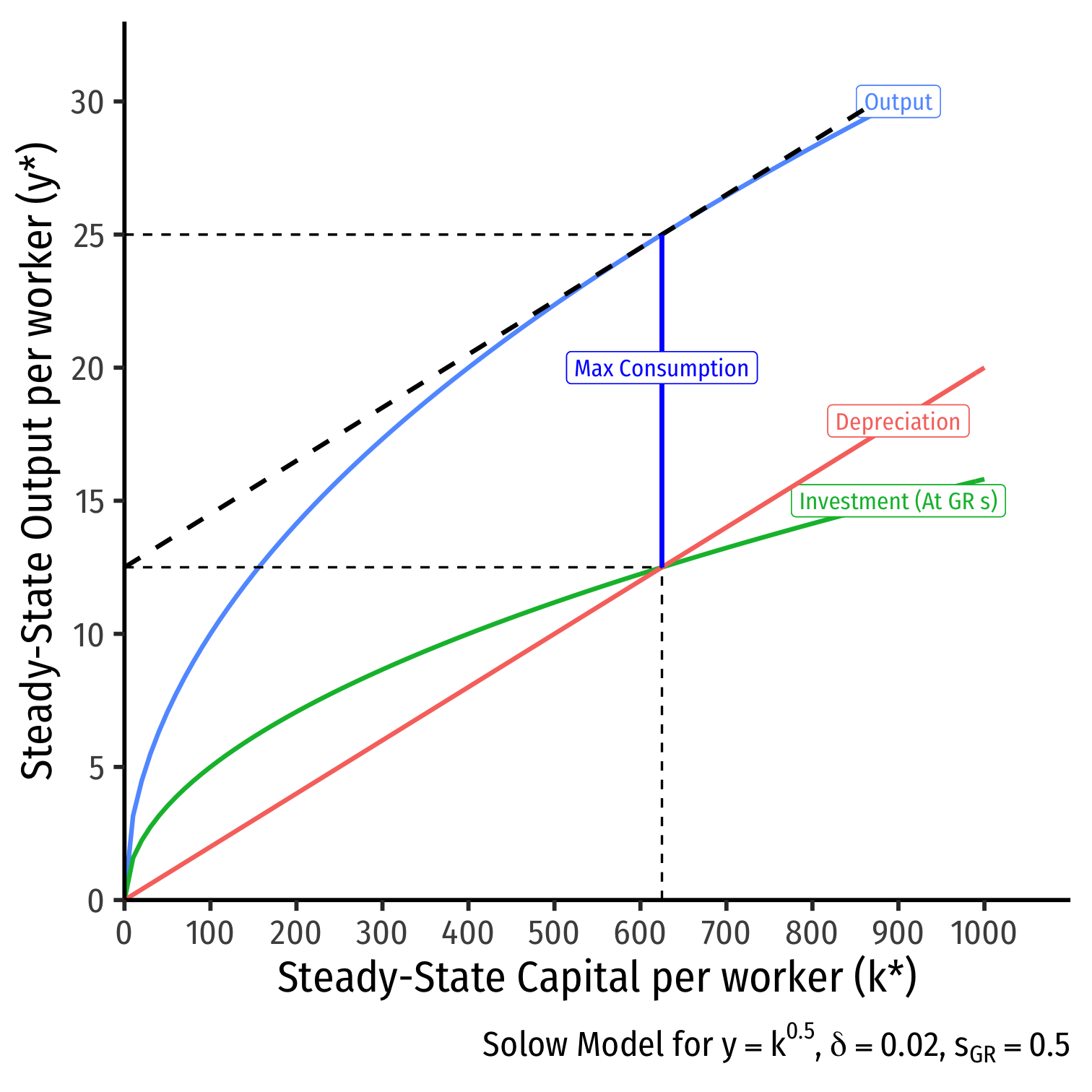
The Golden Rule Level of k IV

  • Policy implications: policymakers can choose s to maxc∗i at k∗GR

  • Change taxes or government spending

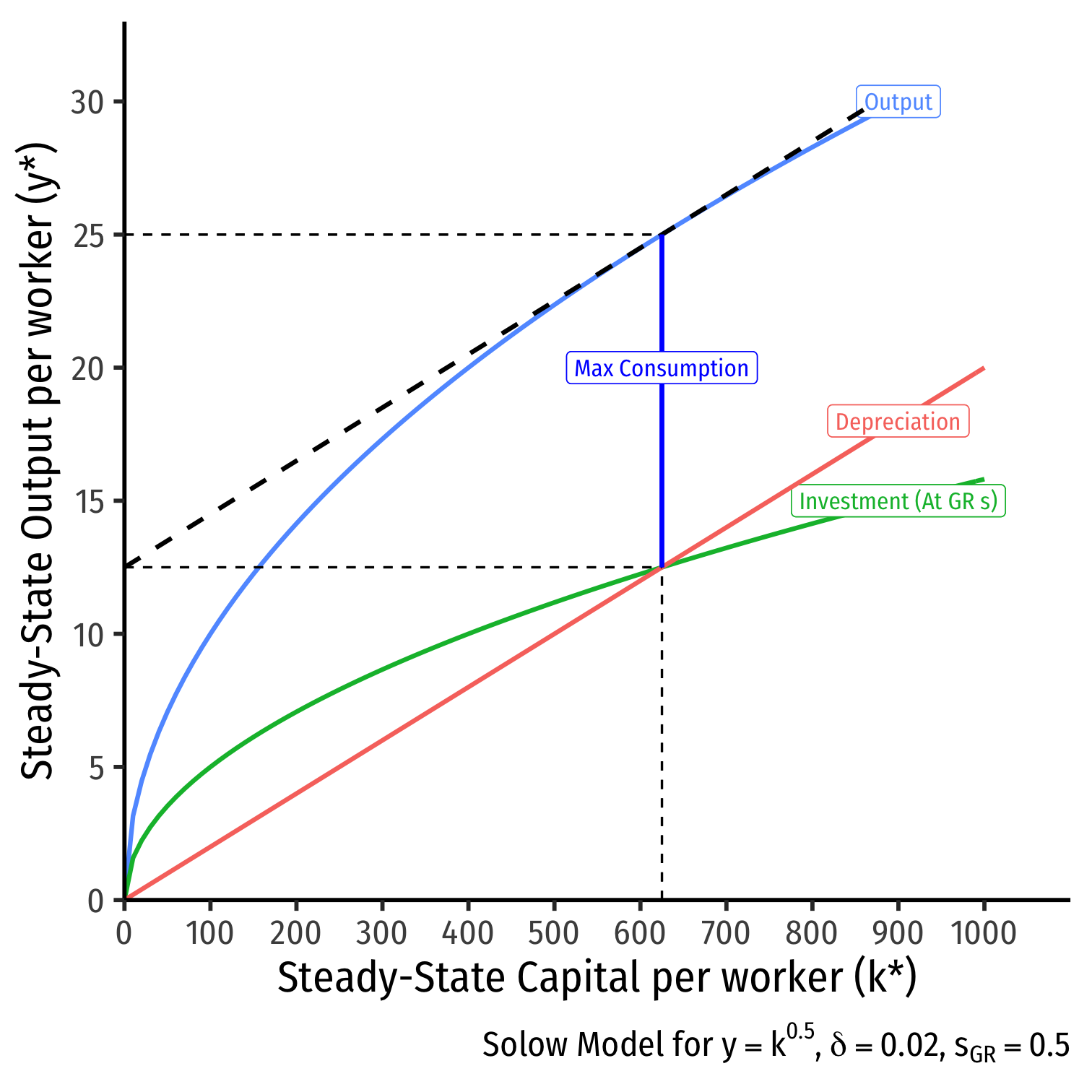
Main Properties of the Solow Model

  1. There exists a unique steady state capital to labor ratio, k∗

    • Where investment = depreciation
    • sf(k)=δ(k)

  2. Higher savings rate s implies a higher steady state value of k∗

  3. An economy converges over time to the steady state level of k∗

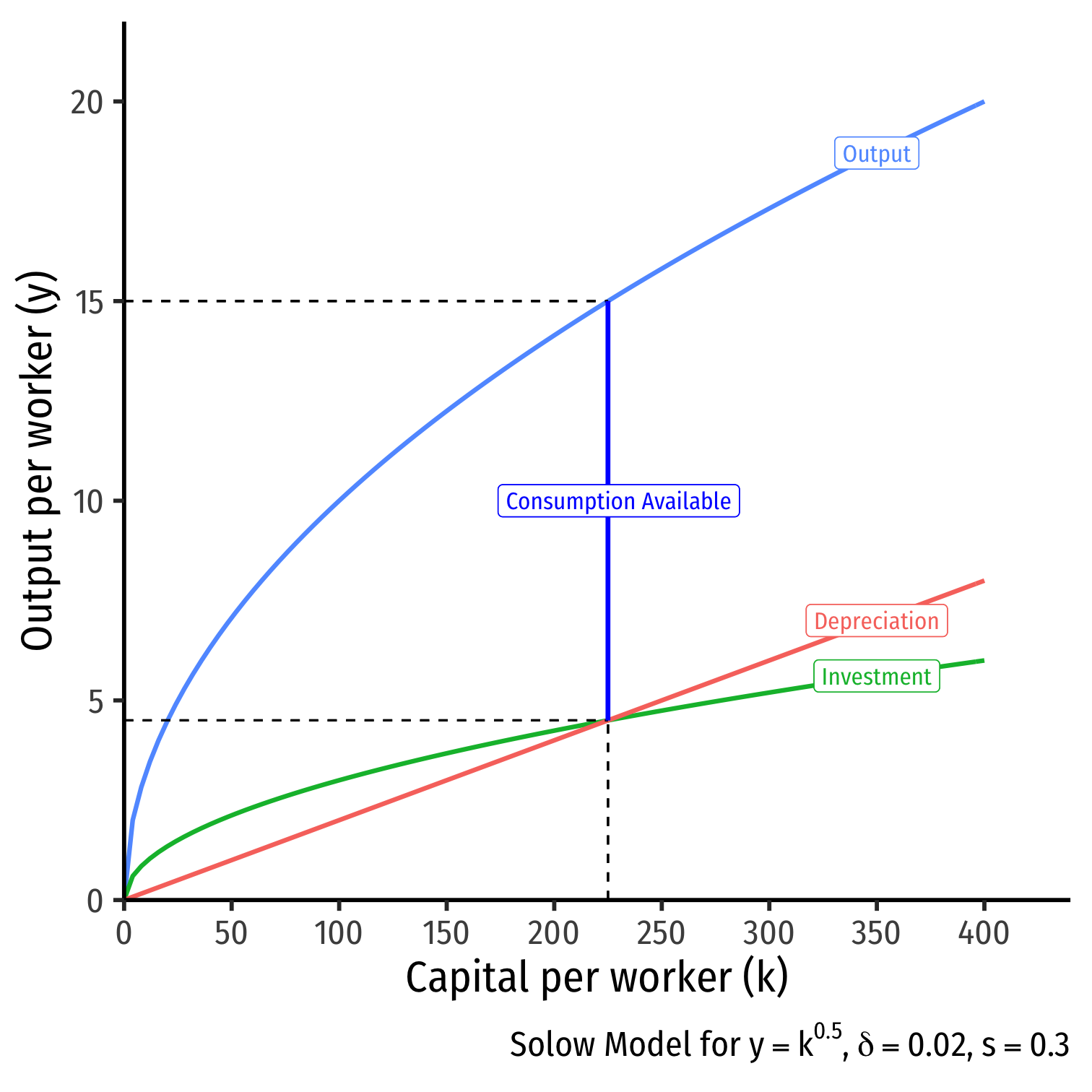
The "Simple" Solow Model and Kaldor's Facts

  1. In steady state, gy=0 and gk=0: output and capital (per worker) do now grow!

  2. The only explanation that fits with Kaldor's facts (1-2) is that all countries must be BELOW their steady states

  3. Growth would have to be slowing down over time

  • These are motivations for the "full Solow" model

The "Full" Solow Model I

  • Add two new "laws of motion" beyond just capital:

  • Population grows at constant rate n over time

    • Lt+1=Lt(1+n)
    • gL=n

  • Technology grows at constant rate g over time

    • At+1=At(1+g)
    • gA=g (g is the growth rate of technology)

  • Redefine k≡KtAtLt as capital per effective worker

    • Labor is being augmented by technology, hence At×Lt
    • At+1Lt+1=AtLt(1+n)(1+g)

The "Full" Solow Model II

  • Long story short, our new takeaway implications:

  1. Δk=sf(kt)−(δ+n+g)kt

    • Capital per effective worker is equal to investment (first term) minus break-even investment

  2. Break even investment: (δ+n+g)k

    • Amount of investment necessary to keep k constant, consists of:
      • δk: to replace capital depreciation
      • nk: to provide capital to new workers
      • gk: to provide capital for new "effective workers" created by technology

The "Full" Solow Model: Graphically I

  • Whenever Investment = Break-even Investment

    • Capital stock reaches a steady state, gK=0
    • Adding exactly as much new capital that is needed to break-even
    • No movement on graph

  • Steady State level of capital: k∗t:sf(kt)=(δ+n+g)kt,gk=0

  • Steady State level of output

    • Amount available for consumption, c∗t=y∗t−i∗t

The "Full" Solow Model: Graphically II

  • Growth rates in the steady state:
Variable Symbol Growth Rate
Capital per effective worker k=KAL 0
Output per effective worker y=YAL 0
Output per worker YL=Ay g
TFP A g
Labor (population) L n
Total Capital K=ALk n+g
Total Output Y=yAL n+g
  • Interesting: growth rate of output per worker grows solely from rate of TFP progress (g)!

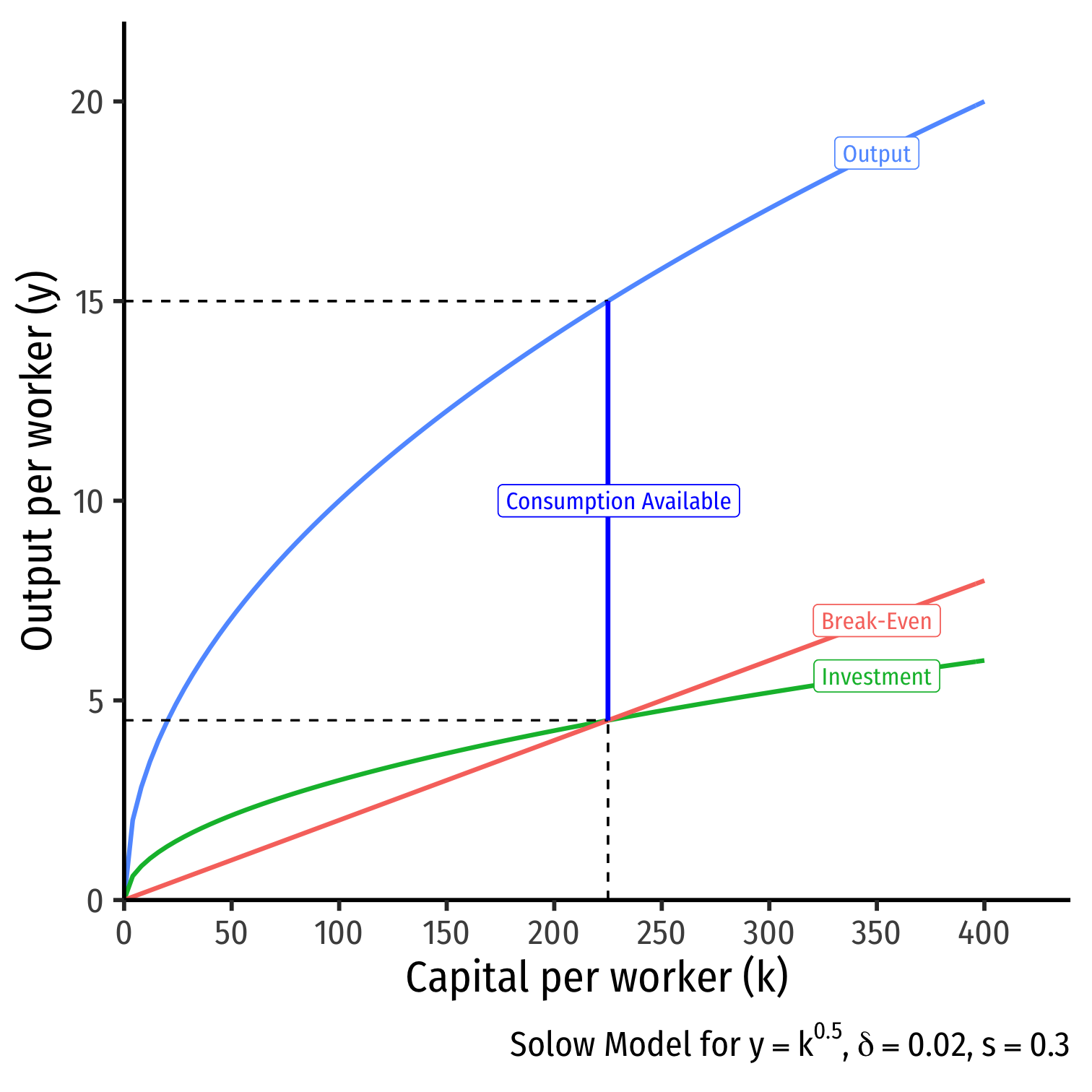
The "Full" Solow Model and Kaldor's Facts

  1. Output per worker grows at rate g (Kaldor's Fact 1)

  2. Capital per worker grows at rate g (Kaldor's Fact 2)

  3. Capital and output grow at the same rate over time (Kaldor's Fact 3)

  4. Capital and labor's share of output (α and 1−α, respectively) do not change over time (Kaldor's Fact 4)

  5. The return to capital is constant (it can be shown to be r=α(k∗)α−1)

  • What about Kaldor's Fact 6: levels of output per worker vary widely across countries?

Cross-Country Comparisons

Solow Model Cross-Country Comparisons: Convergence

  • All else equal, poor countries (low YL and KL) should grow faster than rich ones (high YL and KL)

  • Income gap between wealthy and poor countries should cause living standards to converge over time

Convergence: Technical

  • Near the balanced growth path k→(k∗) at a speed proportional to its distance from k∗:

k(t)≈k∗+e−[1−αk∗](n+g+δ)t(k0−k∗)

  • In other words - the further away from (closer to) k∗ your country is, the faster (slower) you should grow

Convergence? I

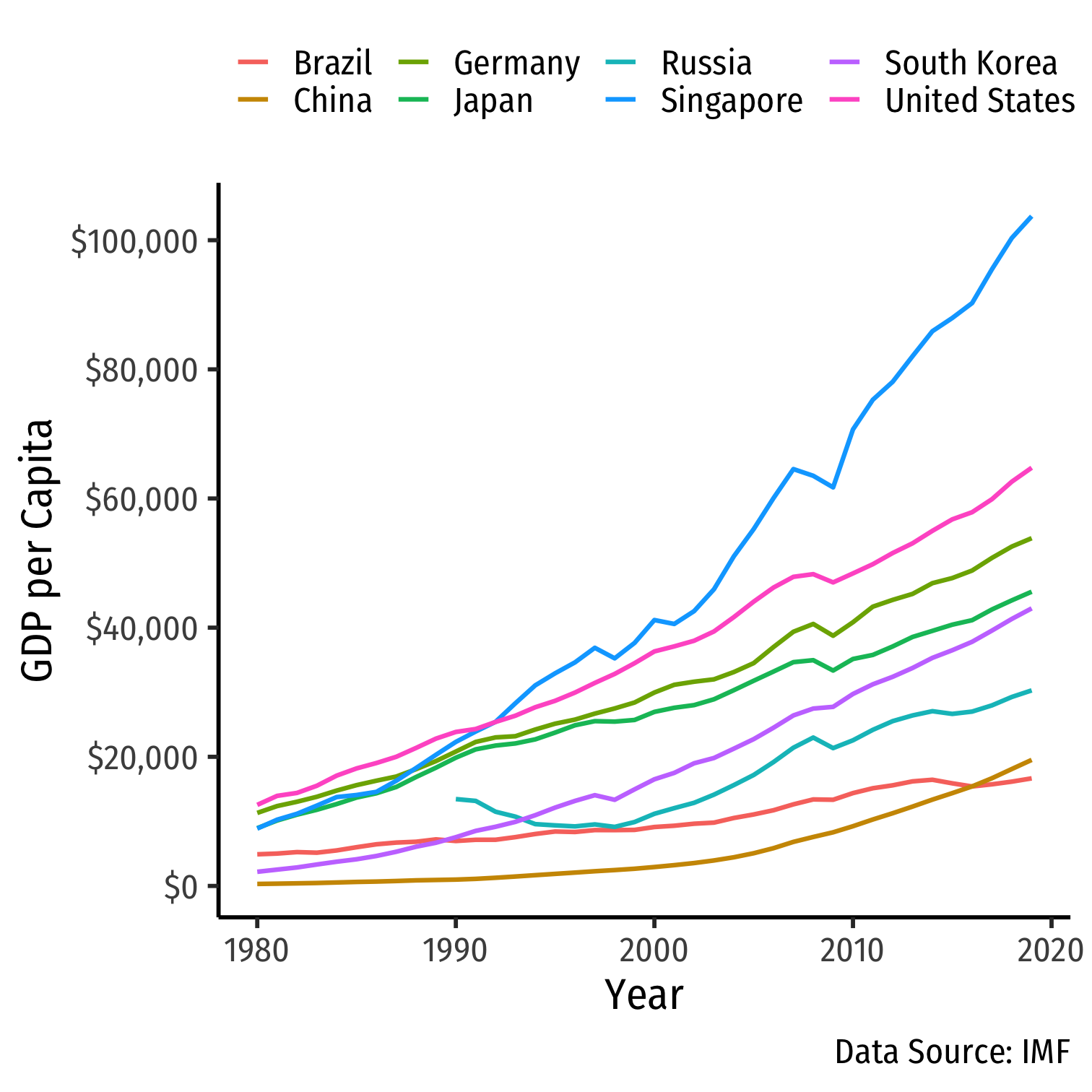
Convergence? II

James Bessen

1958-

"By the early twentieth century, British textile equipment manufacturers were shipping power looms and other textile equipment around the globe. Mills in India, China, and elsewhere not only used the same equipment as British mills, but they were often run by experienced British managers aided by British master weavers and spinners and engineers. Nevertheless, their output per worker was far less than that of the English or American mills because their workers -- using the exact same machines -- lacked the same knowledge and skills. Western weavers were 6.5 times more productive. The English and American cotton textile industries held a sustained economic advantage for decades, despite paying much higher wages," (pp.18-19).

Bessen, James, 2015, Learning by Doing: The Real Connection between Innovation, Wages, and Wealth, New Haven, CT: Yale University Press

Convergence? III

James Bessen

1958-

"[T]he technical knowledge needed to install, manage, and operate this technology, along with the necessary institutiosn and organizations to allow large numbers of workers to acquire this knowledge, did not appear in these countries for many decades. Cotton textile workers in China, India, and Japan in 1910 had the same machines as those in England, but their productivity was far less than that of the English or American workers because they lacked the same knowledge and skills. Even when English managers ran mills in India and China, productivity tended to be low because the English managers had to adapt their knowledge to a different environment and culture.," (p.98).

Bessen, James, 2015, Learning by Doing: The Real Connection between Innovation, Wages, and Wealth, New Haven, CT: Yale University Press

Convergence? IV

  • All else is not equal!

  • Solow model predicts conditional convergence: countries converge to their own steady states determined by saving, population growth, and education (s,n,g)

  • IF countries had similar institutions, then they should converge

From MR University

Conditional Convergence

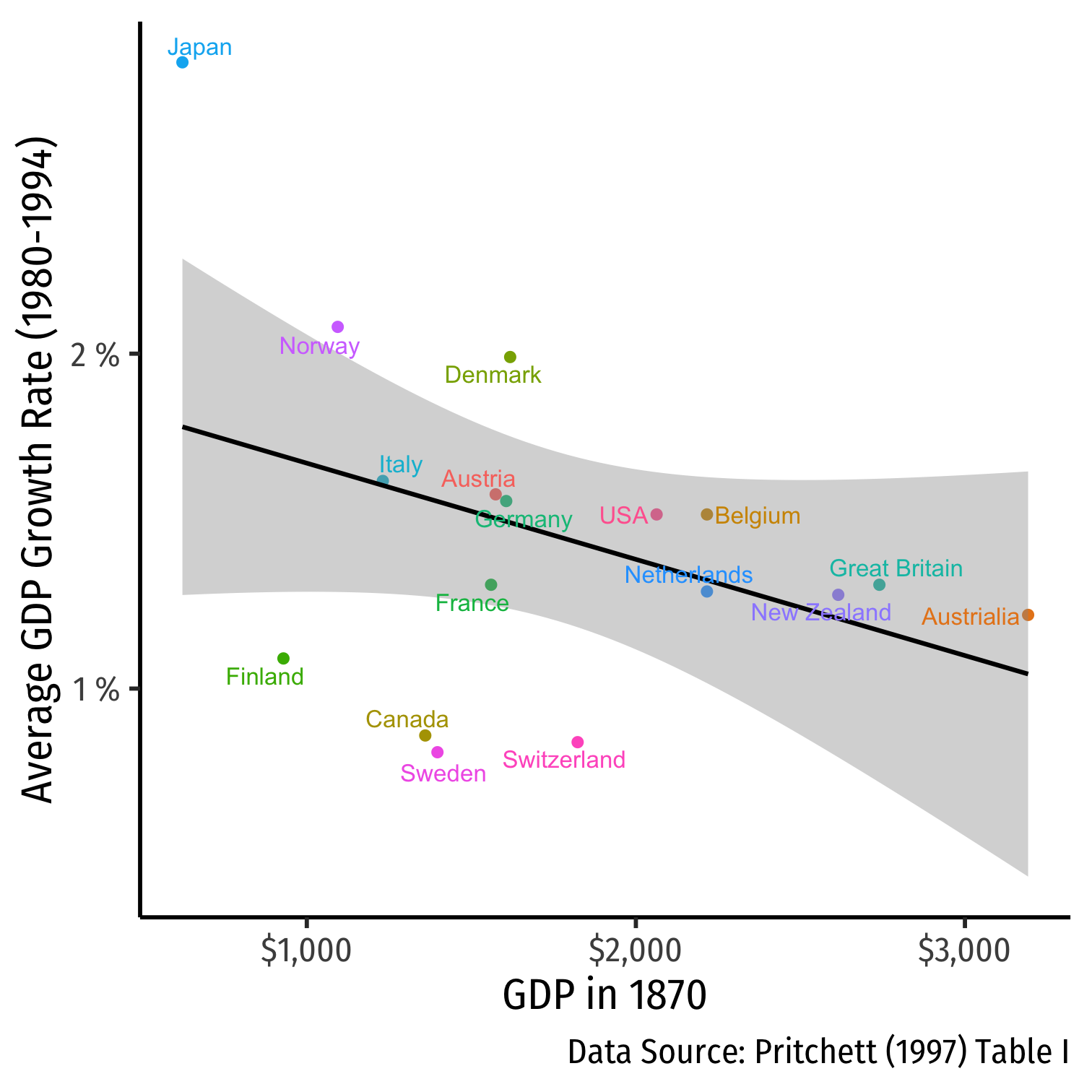
Pritchett, Lant, 1997, "Divergence, Big Time," Journal of Economic Perspectives 11(3): 3-17

Divergence, Big Time

"[F]rom 1870 to 1990 the ratio of per capita incomes between the richest and the poorest countries increased by roughly a factor of five and that the difference in income between the richest country and all others has increased by an order of magnitude."

Pritchett, Lant, 1997, "Divergence, Big Time," Journal of Economic Perspectives 11(3): 3-17

Convergence, Big Time?

"While unconditional convergence was singularly absent in the past, there has been unconditional convergence, beginning (weakly) around 1990 and emphatically for the last two decades."

Johnson, Paul and Chris Papageorgiou, 2018, "What Remains of Cross-Country Convergence?" Journal of Economic Literature, forthcoming

Convergence

  • Consider two types of economic growth

  • "Cutting-edge Growth"

    • tends to be much slower
    • has to push out the PPF with new innovation and progress

  • "Catching-up Growth"

    • tends to be much faster
    • can mimic and import existing innovation from other countries

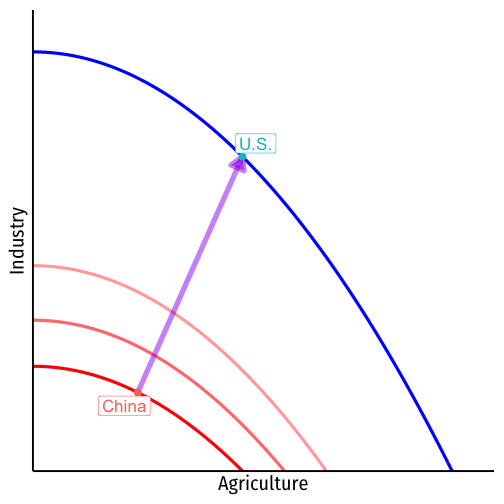
Growth on the Frontier is Hard I

Source: The Atlantic (Nov 16, 2018)

Source: Freakonomics (Nov 29, 2017)

Growth on the Frontier is Hard II

Growth Accounting

The Solow Model: Growth Accounting I

gY=FAAY∗gA+αgK+(1−α)gL

  • Output growth gY can be explained as the growth of "technology" gA and the growth of factors (αgK+(1−α)gL)1

The Solow Model: Growth Accounting I

gY=FAAY∗gA+αgK+(1−α)gL

  • Output growth gY can be explained as the growth of "technology" gA and the growth of factors (αgK+(1−α)gL)1

  • Used to determine how much of total output can be explained by growth in factors and "everything else," known as the Solow Residual - often interpreted as "technology"

The Solow Model: Growth Accounting I

gY=FAAY∗gA+αgK+(1−α)gL

  • Output growth gY can be explained as the growth of "technology" gA and the growth of factors (αgK+(1−α)gL)1

  • Used to determine how much of total output can be explained by growth in factors and "everything else," known as the Solow Residual - often interpreted as "technology"

  • We can directly measure (roughly) Y,L,K and α, but not FAAY, the Solow residual

    • Measure it as Solow Residual=gY−αgK−(1−α)gL

1 All g's stand for growth rates, or percentage change, of the relevant variable (Y,A,K,L). See the class notes page for a derivation of Growth Accounting based on Solow (1957)

Solow, Robert, 1957, "Technical Change and the Aggregate Production Function," The Review of Economics and Statistics 39(3): 312-320

The Solow Model: Growth Accounting II

Robert Solow

(1924-)

Economics Nobel 1987

Solow, Robert, 1957, "Technical Change and the Aggregate Production Function," The Review of Economics and Statistics 39(3): 312-320

The Solow Model: Growth Accounting III

Robert Solow

(1924-)

Economics Nobel 1987

Solow's findings for 1909-1949 in the United States:

  1. Output per worker grew by about 100%
  2. Capital-to-labor ratio grew by about 30% ("capital-deepening")
  3. Technology grew by about 87.5%
    • i.e. 87.5% of the growth in output per worker came from Technology; 12.5% from increases in capital per worker
  4. Measure of Technology fell in a number of recession/depression years and rose during expansions -- technology is "pro-cyclical"
  5. Aggregate production function displays a positive and diminishing marginal product of capital

Solow, Robert, 1957, "Technical Change and the Aggregate Production Function," The Review of Economics and Statistics 39(3): 312-320

The Solow Model: Growth Accounting IV

Growth Accounting: TFP

Exogenous Growth, With Human Capital I

  • Solow model(s) can't account for all differences between countries (based on KL ratio)

  • What about if we add human capital - skills and education embodied in people, such that it augments labor productivity?

Exogenous Growth, With Human Capital II

Yt=Kαt(AtHt)1−α

  • Replacing L with AH

  • A again grows at (exogenous) rate gA=g

  • Ht=LtG(E)

    • Labor Lt is affected by G(E), where E is .shout[education]
    • G(E) is the function that describes how education affects labor Lt

  • How to model G(E)?

Exogenous Growth, With Human Capital II

Yt=Kαt(AtHt)1−α

  • How to model G(E)?

  • Presumably positive (more education ⟹ more human capital)

  • Diminishing returns? Signalling theory of education?

Exogenous Growth, With Human Capital III

Yt=Kαt(AtHt)1−α

  • The dynamics of this model are virtually identical to Solow's

  • Good: easy to solve

  • Bad: we fail to explain g (still exogenously assumed)

Exogenous Growth, With Human Capital IV

"In 1988 output per worker in the United States was more than 35 times higher than output per worker in Niger. In just over ten days the average worker in the United States produced as much as an average worker in Niger produced in an entire year."

"Differences among countries can be attributed to differences in human capital, physical capital, and productivity...Different capital intensities in the two countries contributed a factor of 1.5 to the income differences, while different levels of educational attainment contributed a factor of 3.1. The remaining difference - a factor of 7.7 remains as the productivity residual, (p.83).

Hall, Robert E, and Charles I Jones, 1999, "Why Do Some Countries Produce So Much More Output Per Worker Than Others?" Quarterly Journal of Economics 114(1): 83-116

Exogenous Growth, With Human Capital V

"Our hypothesis is that differences in capital accumulation, productivity, and therefore output per worker are fundamentally related to differences in social infrastructure across countries. By social infrastructure we mean the institutions and government policies that determine the economic environment within which individuals accumulate skills, and firms accumulate capital and produce output," (p. 84).

Hall, Robert E, and Charles I Jones, 1999, "Why Do Some Countries Produce So Much More Output Per Worker Than Others?" Quarterly Journal of Economics 114(1): 83-116

Endogenous Growth

The Romer Model I

Paul Romer

(1955-)

Economics Nobel 2018

"Growth in this model is driven by technological change that arises from intentional investment decisions made by profit-maximizing agents. The distinguishing feature of the technology as an input is that it is neither a conventional good nor a public good; it is a non-rival, partially excludable good. Because of the nonconvexity introduced by a nonrival good, price-taking competition cannot be supported. Instead, the equilibrium is one with monopolistic competition.

"The main conclusions are that the stock of human capital determines the rate of growth, that too little human capital is devoted to research in equilibrium, that integration into world markets will increase growth rates, and that having a large population is not sufficient to generate growth," (pp.S71).

Romer, Paul M, 1990, "Endogenous Technological Change," Journal of Political EConomy 98(5-2): S71-S102

Aside: Paul Romer

Source: New York Times: Sept 5, 2019

Source: Financial Times: Jan 25, 2018

The Romer Model II

Paul Romer

(1955-)

Economics Nobel 2018

  • We'll explore the features of Romer's model, equations and graphs are far too complicated1

  • Romer's model builds on 30 years of macro models since Solow (1956):

1 But otherwise, his first 8 pages are quite easy and enjoyable to read!

Macro Models In the 30 Years Since Solow (1956)

  • Ramsey-Kass-Koopmans model (1965): Solow model with microfoundations!
    • Savings rate s is endogenized:
    • "infinitely-lived" utility-maximizing individuals decide to supply labor and rent capital to cost-minimizing firms in order to earn income, which they can consume and save for future periods
    • single steady state equilibrium
    • groundwork for all modern macro dynamic stochastic general equilibrium (DSGE) models

Macro Models In the 30 Years Since Solow (1956)

  • Ramsey-Kass-Koopmans model (1965): Solow model with microfoundations!

    • Savings rate s is endogenized:
    • "infinitely-lived" utility-maximizing individuals decide to supply labor and rent capital to cost-minimizing firms in order to earn income, which they can consume and save for future periods
    • single steady state equilibrium
    • groundwork for all modern macro dynamic stochastic general equilibrium (DSGE) models

  • Overlapping Generations (Diamond) model (1965):

    • Individuals live for 2 periods only (work and retire), determine the savings rate
    • Multiple steady state equilibria possible
    • Economy subject to dynamic inefficiency

The Motivations for Romer

  • Problems with how Solow models the aggregate economy:

  1. "Knowledge" (TFP) has a non-rival component to it

  2. Markets/aggregate production function cannot possibly be competitive and constant returns to scale

    • Market power/monopolistic competition
    • Increasing returns to scale

  3. Knowledge does not grow exogenously, but is the result of market forces and optimizing choices: people and firms face incentives to create and exploit it (or not)

Digression: The Economics of Ideas

The Economic Problem with Ideas I

The Economic Problem with Ideas I

Rivalrous Nonrival
Excludable PRIVATE GOODS COMMON RESOURCES
(Houses, Jeans) (Fisheries, Environment)
Nonexcludable CLUB GOODS PUBLIC GOODS
(Wifi, Cable TV) (Asteroid Defense)

The Economic Problem with Ideas II

Thomas Jefferson

(1743-1826)

"He who receives an idea from me, receives instruction himself without lessening mine; as he who lights his taper at mine, receives light without darkening me. That ideas should freely spread from one to another over the globe, for the moral and mutual instruction of man, and improvement of his condition, seems to have been peculiarly and benevolently designed by nature, when she made them, like fire, expansible over all space, without lessening their density in any point, and like the air in which we breathe, move, and have our physical being, incapable of confinement or exclusive appropriation."

Jefferson, Thomas, 13 Aug 1813, "Letter to Isaac MacPherson,"

The Economic Problem with Ideas II

Thomas Macaulay

(1800-1859)

"It is then on men whose profession is literature, and whose private means are not ample, that you must rely for a supply of valuable books. Such men must be remunerated for their literary labour...It is desirable that we should have a supply of good books; we cannot have such a supply unless men of letters are liberally remunerated, and the least objectionable way of remunerating them is by means of copyright...The system of copyright has great advantages, and great disadvantages...Copyright is monopoly, and produces all the effects which the general voice of mankind attributes to monopoly...Monopoly is an evil...For the sake of the good we must submit to the evil; but the evil ought not to last a day longer than is necessary for the purpose of securing the good..."

Macaulay, Thomas, 1841 Parliamentay speech against Serjeant Talfourd's 1841 Copyright Bill

High Fixed Costs, Low Marginal Costs I

  • It costs about $1,000,000,000 and 10 years on average to create a new drug. Once discovered, it costs the firm (or it's competitors!) about $0.50/pill to manufacture.

High Fixed Costs, Low Marginal Costs II

High Fixed Costs, Low Marginal Costs II

Source: Washington Post (Sept 8, 2017)

Positive Spillovers

William Nordhaus

(1941-)

Economics Nobel 2018

"We conclude that [about 2.2%] of the social returns from technological advances over the 1948-2001 period was captured by producers, indicating that most of the benefits of technological change are passed on to consumers rather than captured by producers," (p.1)

Nordhaus, William, 2004, "Schumpeterian Profits in the American Economy: Theory and Measurement," NBER Working Paper 10433

Property Rights in Innovation

  • For these economic reasons, patent (for ideas and inventions) and copyright (for expressions) laws exist

  • Grant temporary monopoly to holder in order to recover their fixed costs and provide incentive to undertake (risky and expensive) research/creativity

  • A utilitarian tradeoff between incentives and access

This Implies Market Power

Paul Romer

(1955-)

Economics Nobel 2018

"If all inputs were paid their value marginal product, the firm would suffer losses," (p.S76).

"There is little doubt that much of the value to society of any given innovation or discovery is not captured by the inventor, and any model that missed these spillovers would miss important elements of the growth process. Yet it is still the case that private, profit-maximizing agents make investments in the creation of new knowledge and that they earn a return on these investments by charging a price for the resulting goods that is greater than the marginal cost of producing the goods," (p.S90).

Romer, Paul M, 1990, "Endogenous Technological Change," Journal of Political EConomy 98(5-2): S71-S102

Are Intellectual Property Rights in the Model?

Paul Romer

(1955-)

Economics Nobel 2018

"Although other assumptions about secrecy and property rights could be considered, the equilibrium here is based on the assumption that anyone engaged in research has free access to the entire stock of knowledge. This is feasible because knowledge is a nonrival input. All researchers can take advantage of A at the same time," (p.S83).

Romer, Paul M, 1990, "Endogenous Technological Change," Journal of Political EConomy 98(5-2): S71-S102

The Romer Model

Romer Model: Assumptions I

  • Population (or labor supply) and the total stock of human capital in the population are fixed (ˉL,ˉH)

  • Four factors of production:

  1. Labor L
  2. Physical capital K
    • a stock of "machines" that can be accumulated
    • diminishing returns
  3. Human capital H
    • rivalrous, embodied in L and K
  4. Technology A
    • nonrival, exists beyond individuals, grow indefinitely
    • a stock, like K, that can be accumulated
    • no restrictions on returns!
    • measured as countable "new designs" for capital

Romer Model: Assumptions II

  • The economy has three sectors:
  1. Research sector
    • Uses inputs H and the existing stock of knowledge At−1 to produce new knowledge, At
    • Measured in "new designs" for capital K

Romer Model: Assumptions II

  • The economy has three sectors:
  1. Research sector
    • Uses inputs H and the existing stock of knowledge At−1 to produce new knowledge, At
    • Measured in "new designs" for capital K
  1. Intermediate goods sector
    • Takes inputs H and At to produce K for use in final goods sector

Romer Model: Assumptions II

  • The economy has three sectors:
  1. Research sector
    • Uses inputs H and the existing stock of knowledge At−1 to produce new knowledge, At
    • Measured in "new designs" for capital K
  1. Intermediate goods sector
    • Takes inputs H and At to produce K for use in final goods sector
  1. Final goods sector
    • uses L, H, and K to produce final output Y

Romer Model: Assumptions II

  • The economy has three sectors:
  1. Research sector
    • Uses inputs H and the existing stock of knowledge At−1 to produce new knowledge, At
    • Measured in "new designs" for capital K
  1. Intermediate goods sector
    • Takes inputs H and At to produce K for use in final goods sector
  1. Final goods sector
    • uses L, H, and K to produce final output Y

  • Output can be consumed, or saved (to be used to make new capital, K): Yt=Ct+St

  • Fixed supply of human capital is allocated to research sector or manufacturing based on relative manufacturing wages and return to new designs ˉH=HA+HY

The Nature of "Knowledge" I

  • Knowledge (A) is a stock that can be accumulated, like physical capital (K)

  • To produce new knowledge, you need to use the existing stock of knowledge

    • i.e. need the idea of gravity to get relativity, we need both to get quantum mechanics, etc.

The Nature of "Knowledge" II

"[A] college-educated engineer working today and one working 100 years ago have the same human capital, which is measured in terms of years of forgone participation in the labor market. The engineer working today is more productive because he or she can take advantage of all of the additional knowledge accumulated as design problems were solved during the last 100 years," (pp. S83-S84).

The Nature of "Knowledge" III

ΔA=δHAA

  • δ: a productivity parameter

  • HA: fraction of human capital available (ˉH) allocated to research

  • Knowledge need not exhibit constant returns to scale

  • Would doubling human capital and doubling the existing stock of knowledge lead to twice the new knowledge produced?

The Nature of "Knowledge" IV

  • Takeaways from knowledge:

  1. Devoting more human capital to research (HA) leads to more knowledge ΔA

  2. The larger the total stock of knowledge (A), the higher the productivity of labor in the research sector

The Model's Equilibrium

Paul Romer

(1955-)

Economics Nobel 2018

  • In the model's equilibrium (p.S88):

  1. Consumers decide between C and S based on interest rate r

  2. Holders of H decide whether to work in Research sector (HA) or in Manufacturing (HY) based on existing stock of knowledge A, price of designs, and wages in manufacturing

  3. Final goods producers choose cost-minimizing inputs of L, H, and K

  4. Each firm owning A (designs) sets prices to maximize profit given interest rate and market demand curves in final product market

  5. Potential entrants to market consider price of designs in entry decision

  6. Supply equals demand for each good

Romer, Paul M, 1990, "Endogenous Technological Change," Journal of Political EConomy 98(5-2): S71-S102

Romer Model: Growth Rate

  • As in full Solow model, growth rate of output per worker YL is the growth rate of knowledge (A), i.e. g

  • Main problem with Solow (exogenous) growth model(s): g is assumed as a constant number

  • Romer endogenizes g, sp how does it grow?

Romer Model: Growth Rate

  • As in full Solow model, growth rate of output per worker YL is the growth rate of knowledge (A), i.e. g

  • Main problem with Solow (exogenous) growth model(s): g is assumed as a constant number

  • Romer endogenizes g, sp how does it grow?

g=δH−ΛρσΛ+1

  • Λ=α(1−α−β)(α+β)1
  • δ: a productivity parameter (of H)
  • ρ: discount rate (from Ramsey-Kass-Koopmans model)
  • σ: growth rate of utility (from Ramsey-Kass-Koopmans model)

1 α and β are exponents from Cobb-Douglas production function: Y=HαLβK1−α−β

Romer Model Implication I - R&D Is Critical

  • Economies tend to undersupply human capital to research:

The most obvious reason is that research has positive external effects. An additional design raises the productivity of all future individuals who do research, but because this benefit is nonexcludable, it is not reflected at all in the market price for designs. The second and an equally important reason...is that research produces an input that is purchased by a sector that engages in monopoly pricing. The markup of price over marginal cost forces a wedge between the marginal social product of an input used in this sector and its market compensation," (p.S96)

Romer Model Implication I - R&D Is Critical

  • Economies tend to undersupply human capital to research:

The most obvious reason is that research has positive external effects. An additional design raises the productivity of all future individuals who do research, but because this benefit is nonexcludable, it is not reflected at all in the market price for designs. The second and an equally important reason...is that research produces an input that is purchased by a sector that engages in monopoly pricing. The markup of price over marginal cost forces a wedge between the marginal social product of an input used in this sector and its market compensation," (p.S96)

  • Policy implications:

"Within the confines of the model, the social optimum can be achieved by subsidizing the accumulation of A," (p.S97)

"A subsidy to physical capital accumulation may be a very poor substitute for direct subsidies that increase the incentive to undertake research. In the absence of feasible policies that can remove the divergence between the social and private returns to research, a second-best policy would be to subsidize the accumulation of total human capital," (p.S99)

Romer Model Implication II - Trade Liberalization

  • A large population is not sufficient for greater technology (and thus, economic growth), it requires access to a larger market (division of labor)!

If access to a large number of workers or consumers were all that mattered, having a large population would be a good substitute for trade with other nations. The model here suggests that what is important for growth is integration not into an economy with a large number of people but rather into one with a large amount of human capital, (p.S98)

"The most interesting positive implication of the model is that an economy with a larger total stock of human capital will experience faster growth. This finding suggests that free international trade can act to speed up growth. It also suggests a way to understand what it is about developed economies in the twentieth century that permitted rates of growth of income per capita that are unprecedented in human history. The model also suggests that low levels of human capital may help explain why growth is not observed in underdeveloped economies that are closed and why a less developed economy with a very large population can still benefit from economic integration with the rest of the world," (p.S99)

One Test of the Model: "Market Access" Literature

  • Sokoloff (1988): counties in the U.S. in the 19th century that had access to navigable waterways had higher rates of patenting (proxy for innovation, adding to A) than those that did not
    • Even clearer: counties that gained access to new waterway (i.e. a new canal) saw sharp increase in patenting!

Sokoloff, Kenneth L, 1988, "Inventive Activity in Early Industrial America: Evidence From Patent Records, 1790-1846," NBER Working Paper 2707

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income
  3. "Knowledge" or "TFP" explains the overhelming part of growth differences across the world

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income
  3. "Knowledge" or "TFP" explains the overhelming part of growth differences across the world
  4. Solow model predicts LICs should grow at faster rates than HICs

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income
  3. "Knowledge" or "TFP" explains the overhelming part of growth differences across the world
  4. Solow model predicts LICs should grow at faster rates than HICs
  5. The evidence for (4) is mixed and controversial

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income
  3. "Knowledge" or "TFP" explains the overhelming part of growth differences across the world
  4. Solow model predicts LICs should grow at faster rates than HICs
  5. The evidence for (4) is mixed and controversial
  6. Growth literature suggests economies can grow faster by subsidizing the accumulation of capital, or human capital, or "knowledge"
    • The evidence that we are able to do this, or have been able to, is quite poor

Takeaways from Growth Models

  1. HICs have more output per worker and capital per worker than LICs
  2. The accumulation of physical capital itself explains a very small part of differences in income
  3. "Knowledge" or "TFP" explains the overhelming part of growth differences across the world
  4. Solow model predicts LICs should grow at faster rates than HICs
  5. The evidence for (4) is mixed and controversial
  6. Growth literature suggests economies can grow faster by subsidizing the accumulation of capital, or human capital, or "knowledge"
    • The evidence that we are able to do this, or have been able to, is quite poor
  7. An economy's "TFP" is more sensitive to its institutions and incentives than simply amassing K or H or A

Takeaways from Growth Models II

Growth Models: An Appraisal

  • For all of their flaws, growth models are part of the "shared" language of development experts, policy makers, and macroeconomists

  • Explain (some) mechanisms of growth that we can model and predict (some) consequence of (some) policy changes

  • Give us a measure of how much we can explain based on what we understand, and how much we cannot explain and need to understand

All models are wrong. Some are useful. - George Box

Growth Models: A History

Working Tools

The Solow (Exogenous) Growth Model

Cross-Country Comparisons

Growth Accounting

Endogenous Growth

Digression: The Economics of Ideas

The Romer Model

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow